题目内容
在120°的二面角内，放置一个半径为3的球，该球切二面角的两个半平面于A、B两点，那么这两个切点的球面上的最短距离为（ ）
| A．π | B．
| C．2π | D．3A |
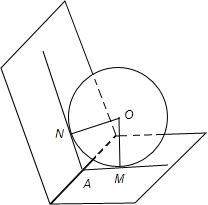
画出图形，如图，在四边形OMNA中，AM、AN是球的大圆的切线，
∴AM⊥OM，AN⊥ON，
∵∠MAN=120°∴∠MON=60°
∴两切点间的球面距离是
=
×OM=π．
故选A．
∴AM⊥OM，AN⊥ON，
∵∠MAN=120°∴∠MON=60°
∴两切点间的球面距离是
 |
| MN |
| π |
| 3 |
故选A．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
