题目内容
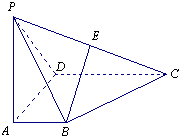
如图,四棱锥P-ABCD的底面ABCD为直角梯形,PA⊥底面ABCD其中AB⊥AD,CD⊥AD,CD=AD=PA=2AB,E是PC中点.
(1)求证:BE∥平面PAD;
(2)求异面直线PD与BC所成角的余弦值.
(1)求证:BE∥平面PAD;
(2)求异面直线PD与BC所成角的余弦值.

(1)取PD中点F,连接EF,AF,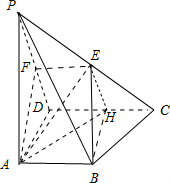
∵E是PC的中点,∴EF
DC,
又∵AB
CD,∴EF
AB,
∴四边形ABEF是平行四边形,∴BE∥AF,
∵BE?平面PAD,AF?平面PAD,
∴BE∥平面PAD.
(2)取CD的中点H,连接AH、EH、AE、BH,
∵AB
CD,∴AB
CH,
∴四边形ABCH为平行四边形,∴BC
AH.
令AB=1,
在Rt△ADH中,由勾股定理得AH=
=
.
∵PA⊥底面ABCD,∴PA⊥AD,
∴PD=2
,AF=
PD=
.
∵四边形ABHD为平行四边形,AD⊥AB,
∴四边形ABHD为矩形,∴AH=
=
.
由三角形的中位线定理可知:EH=
PD=
,
由以上作法可知:∠AHE或其补角即为异面直线PD与BC所成的角.
∵PA⊥AB,AB⊥AD,
∴AB⊥平面PAD,∴AB⊥AF.
又∵四边形ABEF是平行四边形,∴四边形ABEF为矩形,
∴AE=
=
=
.
在△AEH中,由余弦定理得cos∠AHE=
=
.
因此异面直线PD与BC所成角的余弦值为
.

∵E是PC的中点,∴EF
| ∥ |
| . |
| 1 |
| 2 |
又∵AB
| ∥ |
| . |
| 1 |
| 2 |
| ∥ |
| . |
∴四边形ABEF是平行四边形,∴BE∥AF,
∵BE?平面PAD,AF?平面PAD,
∴BE∥平面PAD.
(2)取CD的中点H,连接AH、EH、AE、BH,
∵AB
| ∥ |
| . |
| 1 |
| 2 |
| ∥ |
| . |
∴四边形ABCH为平行四边形,∴BC
| ∥ |
| . |
令AB=1,
在Rt△ADH中,由勾股定理得AH=
| 22+12 |
| 5 |
∵PA⊥底面ABCD,∴PA⊥AD,
∴PD=2
| 2 |
| 1 |
| 2 |
| 2 |
∵四边形ABHD为平行四边形,AD⊥AB,
∴四边形ABHD为矩形,∴AH=
| 12+12 |
| 2 |
由三角形的中位线定理可知:EH=
| 1 |
| 2 |
| 2 |
由以上作法可知:∠AHE或其补角即为异面直线PD与BC所成的角.
∵PA⊥AB,AB⊥AD,
∴AB⊥平面PAD,∴AB⊥AF.
又∵四边形ABEF是平行四边形,∴四边形ABEF为矩形,
∴AE=
| AF2+EF2 |
(
|
| 3 |
在△AEH中,由余弦定理得cos∠AHE=
(
| ||||||
2
|
| ||
| 5 |
因此异面直线PD与BC所成角的余弦值为
| ||
| 5 |

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目