题目内容
8.数列1$\frac{1}{2}$,3$\frac{1}{4}$,5$\frac{1}{8}$,7$\frac{1}{16}$,9$\frac{1}{32}$,…的前n项之和等于${n}^{2}+1-\frac{1}{{2}^{n}}$.分析 把数列1$\frac{1}{2}$,3$\frac{1}{4}$,5$\frac{1}{8}$,7$\frac{1}{16}$,9$\frac{1}{32}$,…的前n项之和,分组[1+3+5+…+(2n-1)]+$[\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n}}]$,利用等差数列与等比数列的前n项和公式即可得出.
解答 解:数列1$\frac{1}{2}$,3$\frac{1}{4}$,5$\frac{1}{8}$,7$\frac{1}{16}$,9$\frac{1}{32}$,…的前n项之和
=[1+3+5+…+(2n-1)]+$[\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n}}]$
=$\frac{n(1+2n-1)}{2}$+$\frac{\frac{1}{2}[1-\frac{1}{{2}^{n}}]}{1-\frac{1}{2}}$
=${n}^{2}+1-\frac{1}{{2}^{n}}$.
故答案为:${n}^{2}+1-\frac{1}{{2}^{n}}$.
点评 本题考查了等差数列与等比数列前n项和公式、“分组求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.已知双曲线的一个焦点与抛物线x2=24y的焦点重合,其一条渐近线的倾斜角为30℃,则该双曲线的标准方程为( )
| A. | $\frac{{x}^{2}}{9}-\frac{{y}^{2}}{27}=1$ | B. | $\frac{{y}^{2}}{9}-\frac{{x}^{2}}{27}=1$ | C. | $\frac{{y}^{2}}{12}-\frac{{x}^{2}}{24}=1$ | D. | $\frac{{y}^{2}}{24}-\frac{{x}^{2}}{12}=1$ |
13.已知函数f(x)=$\frac{2b}{{a}^{x}-1}$+b+6,其中,a,b为常数,a>1,b≠0,若f(lglog210)=8,则f(lglg2)的值为( )
| A. | 8 | B. | 4 | C. | -8 | D. | -4 |
20.已知平面区域Ω:$\left\{\begin{array}{l}{(x+2y-1)(x-2y+3)≥0}\\{|x-1|≤3}\end{array}\right.$,则Ω的面积为( )
| A. | 11 | B. | 13 | C. | 15 | D. | 17 |
17.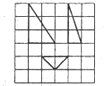 如图,网格纸中的小正方形的边长为1,图中组线画出的是一个几何体的三视图,则这个几何体的表面积为( )
如图,网格纸中的小正方形的边长为1,图中组线画出的是一个几何体的三视图,则这个几何体的表面积为( )
 如图,网格纸中的小正方形的边长为1,图中组线画出的是一个几何体的三视图,则这个几何体的表面积为( )
如图,网格纸中的小正方形的边长为1,图中组线画出的是一个几何体的三视图,则这个几何体的表面积为( )| A. | $\frac{1}{2}$($\sqrt{22}+3\sqrt{2}+4$) | B. | $\frac{1}{2}$($\sqrt{22}+3\sqrt{2}+8$) | C. | $\frac{1}{2}$($\sqrt{22}+\sqrt{2}+8$) | D. | $\frac{1}{2}$($\sqrt{22}+2\sqrt{2}+8$) |
18.一个几何体的三视图如图所示,那么这个几何体的体积为( )


| A. | 16π | B. | 6π | C. | 4π | D. | 8 |