题目内容
18.已知三棱锥P-ABC的顶点P在平面ABC内的射影为点H,侧棱PA=PB=PC,点O为三棱锥P-ABC的外接球O的球心,AB=8,AC=6,已知$\overrightarrow{AO}=λ\overrightarrow{AB}+μ\overrightarrow{AC}+\frac{1}{1+\sqrt{5}}\overrightarrow{HP}$,且μ+2λ=1,则球O的表面积为81π.分析 确定球心在PH上,由PH⊥AB,PH⊥AC,则$\overrightarrow{HP}$•$\overrightarrow{AB}$=$\overrightarrow{HP}$•$\overrightarrow{AC}$=0,对$\overrightarrow{AO}=λ\overrightarrow{AB}+μ\overrightarrow{AC}+\frac{1}{1+\sqrt{5}}\overrightarrow{HP}$,两边取点乘向量AB,向量AC,向量AH,以及两边平方,运用向量的数量积的性质,计算即可得到半径R,再由球的表面积公式计算即可得到.
解答  解:由于三棱锥P-ABC的顶点P在平面ABC内的射影为点H,
解:由于三棱锥P-ABC的顶点P在平面ABC内的射影为点H,
O为球心,OA=OB=OC=OP=R,
即有PH⊥AB,PH⊥AC,
$\overrightarrow{HP}$•$\overrightarrow{AB}$=$\overrightarrow{HP}$•$\overrightarrow{AC}$=0,
由$\overrightarrow{AO}=λ\overrightarrow{AB}+μ\overrightarrow{AC}+\frac{1}{1+\sqrt{5}}\overrightarrow{HP}$,①
则有$\overrightarrow{AO}$•$\overrightarrow{AB}$=$λ{\overrightarrow{AB}}^{2}$+$μ\overrightarrow{AC}•\overrightarrow{AB}$+$\frac{1}{1+\sqrt{5}}\overrightarrow{HP}•\overrightarrow{AB}$,
即有|$\overrightarrow{AB}$|•$\frac{1}{2}$|$\overrightarrow{AB}$|=$λ{\overrightarrow{AB}}^{2}$+$μ\overrightarrow{AC}•\overrightarrow{AB}$,
即32=64λ+$μ\overrightarrow{AC}•\overrightarrow{AB}$,②
同理对①两边取点乘$\overrightarrow{AC}$,可得
18=36μ+λ$\overrightarrow{AB}•\overrightarrow{AC}$,③
又μ+2λ=1④
由②③④解得,λ=$\frac{9}{20}$($\frac{1}{2}$舍去),μ=$\frac{1}{10}$,$\overrightarrow{AB}•\overrightarrow{AC}$=32,
即有$\overrightarrow{AO}$=$\frac{9}{20}$$\overrightarrow{AB}$+$\frac{1}{10}$$\overrightarrow{AC}$+$\frac{1}{1+\sqrt{5}}$$\overrightarrow{HP}$.
即有$\overrightarrow{AO}$$•\overrightarrow{AH}$=$\frac{9}{20}$$\overrightarrow{AB}$•$\overrightarrow{AH}$+$\frac{1}{10}$$\overrightarrow{AC}$$•\overrightarrow{AH}$+$\frac{1}{1+\sqrt{5}}$$\overrightarrow{HP}$$•\overrightarrow{AH}$,
即为AH2=$\frac{9}{20}$×32+$\frac{1}{10}$×18=$\frac{81}{5}$,
又$\overrightarrow{AO}$2=($\frac{9}{20}$$\overrightarrow{AB}$+$\frac{1}{10}$$\overrightarrow{AC}$+$\frac{1}{1+\sqrt{5}}$$\overrightarrow{HP}$)2,
即R2=$\frac{81}{400}$×64+$\frac{1}{100}$×36+($\frac{1}{1+\sqrt{5}}$)2HP2+2×$\frac{9}{200}$×$\overrightarrow{AB}•\overrightarrow{AC}$
=$\frac{81}{5}$+($\frac{1}{1+\sqrt{5}}$)2HP2,⑤
又在直角三角形AOH中,
R2=(HP-R)2+AH2,即有HP2-2HP•R+$\frac{81}{5}$=0,
即为(HP-R)2=R2-$\frac{81}{5}$⑥
由⑤⑥解得R=$\frac{9}{2}$,
则有球O的表面积S=4πR2=81π.
故答案为:81π.
点评 本题考查球的表面积的求法,关键是求得球的半径,同时考查向量的数量积的定义和性质,通过两边取点乘和两边平方法,是解题的重点,具有一定的运算量,属于难题.

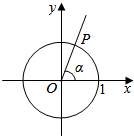 直角坐标系xOy中,锐角α的终边与单位圆的交点为P,将OP绕O逆时针旋转到OQ,使∠POQ=α,其中Q是OQ与单位圆的交点,设Q的坐标为(x,y).
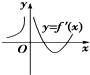
直角坐标系xOy中,锐角α的终边与单位圆的交点为P,将OP绕O逆时针旋转到OQ,使∠POQ=α,其中Q是OQ与单位圆的交点,设Q的坐标为(x,y). 设函数f(x)在定义域内可导且其图象如图①所示,则导函数y=f′(x)的图象最有可能是( )
设函数f(x)在定义域内可导且其图象如图①所示,则导函数y=f′(x)的图象最有可能是( )


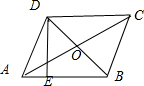 如图所示,?ABCD的对角线AC与BD相交于点O,且AC=4,BD=2$\sqrt{3}$,AB=$\sqrt{7}$,过点D作DE⊥AB,垂足为E.请问四边形ABCD是菱形吗?请说明理由.
如图所示,?ABCD的对角线AC与BD相交于点O,且AC=4,BD=2$\sqrt{3}$,AB=$\sqrt{7}$,过点D作DE⊥AB,垂足为E.请问四边形ABCD是菱形吗?请说明理由.