题目内容
16.已知动点P到定点F(2,0)的距离和它到定直线x=4的距离的比值为$\frac{{\sqrt{2}}}{2}$.(Ⅰ)求动点P的轨迹Ω的方程;
(Ⅱ)若过点F的直线与点P的轨迹Ω相交于M,N两点(M,N均在y轴右侧),点A(0,2)、B(0,-2),设A,B,M,N四点构成的四边形的面积为S,求S的取值范围.
分析 (I)设动点P(x,y),利用两点之间的距离公式可得$\frac{{\sqrt{{{(x-2)}^2}+{y^2}}}}{|x-4|}=\frac{{\sqrt{2}}}{2}$,化简即可得出.
(II)由(Ⅰ),轨迹Ω是以F(2,0)为焦点,离心率为$\frac{{\sqrt{2}}}{2}$的椭圆,如图,连接OM、ON,设直线MN方程为x=my+2,点M(x1,y1),N(x2,y2),与椭圆方程联立消去x,得(m2+2)y2+4my-4=0,利用根与系数的关系可得:S=S△OAM+S△OBN+S△OMN=$\frac{1}{2}×2({x_1}+{x_2})+\frac{1}{2}×2|{y_1}-{y_2}|$=m(y1+y2)+4+|y1-y2|=$-\frac{{4{m^2}}}{{{m^2}+2}}+4+\frac{{4\sqrt{2}•\sqrt{{m^2}+1}}}{{{m^2}+2}}$=$\frac{{4\sqrt{2}•\sqrt{{m^2}+1}+8}}{{{m^2}+2}}$,下面利用导数研究函数的单调性或变形利用基本不等式的性质即可得出.
解答 解:(Ⅰ)设动点P(x,y),则$\frac{{\sqrt{{{(x-2)}^2}+{y^2}}}}{|x-4|}=\frac{{\sqrt{2}}}{2}$,
化简得$\frac{x^2}{8}+\frac{y^2}{4}=1$.
(Ⅱ)由(Ⅰ),轨迹Ω是以F(2,0)为焦点,离心率为$\frac{{\sqrt{2}}}{2}$的椭圆,如图,连接OM、ON,
设直线MN方程为x=my+2,点M(x1,y1),N(x2,y2),
联立$\left\{\begin{array}{l}x=my+2\\ \frac{x^2}{8}+\frac{y^2}{4}=1\end{array}\right.$消去x,得(m2+2)y2+4my-4=0,
则${y_1}+{y_1}=-\frac{4m}{{{m^2}+2}}$,${y_1}{y_1}=-\frac{4}{{{m^2}+2}}$,
∴$|{y_1}-{y_2}|=\sqrt{{{({y_1}+{y_2})}^2}-4{y_1}{y_2}}=\sqrt{{{(-\frac{4m}{{{m^2}+2}})}^2}+\frac{16}{{{m^2}+2}}}=\frac{{4\sqrt{2}•\sqrt{{m^2}+1}}}{{{m^2}+2}}$,
由于M,N均在y轴右侧,则x1>0,x2>0,且0≤|m|<1,
则S=S△OAM+S△OBN+S△OMN=$\frac{1}{2}×2({x_1}+{x_2})+\frac{1}{2}×2|{y_1}-{y_2}|$
=m(y1+y2)+4+|y1-y2|=$-\frac{{4{m^2}}}{{{m^2}+2}}+4+\frac{{4\sqrt{2}•\sqrt{{m^2}+1}}}{{{m^2}+2}}$=$\frac{{4\sqrt{2}•\sqrt{{m^2}+1}+8}}{{{m^2}+2}}$,
方法一、$S'=\frac{{-4\sqrt{2}{t^2}-16t+4\sqrt{2}}}{{{{({t^2}+1)}^2}}}$=$\frac{{-4\sqrt{2}({t^2}+2\sqrt{2}t-1)}}{{{{({t^2}+1)}^2}}}<0$,
故面积函数$S=\frac{{4\sqrt{2}•t+8}}{{{t^2}+1}}$在单调递减,所以$S∈(\frac{16}{3},2\sqrt{2}+4]$,
所以面积S的取值范围是$(\frac{16}{3},2\sqrt{2}+4]$.
方法二、$S=\frac{{4\sqrt{2}(t+\sqrt{2})}}{{{{(t+\sqrt{2})}^2}-2\sqrt{2}t-1}}=\frac{{4\sqrt{2}(t+\sqrt{2})}}{{{{(t+\sqrt{2})}^2}-2\sqrt{2}(t+\sqrt{2})+3}}$=$\frac{{4\sqrt{2}}}{{(t+\sqrt{2})+\frac{3}{{t+\sqrt{2}}}-2\sqrt{2}}}$,
∵$1≤t<\sqrt{2}$,则$(t+\sqrt{2})+\frac{3}{{t+\sqrt{2}}}∈[4\sqrt{2}-2,\frac{{11\sqrt{2}}}{4})$,
∴$(t+\sqrt{2})+\frac{3}{{t+\sqrt{2}}}-2\sqrt{2}∈[2\sqrt{2}-2,\frac{{3\sqrt{2}}}{4})$,
则$\frac{{4\sqrt{2}}}{{(t+\sqrt{2})+\frac{3}{{t+\sqrt{2}}}-2\sqrt{2}}}∈(\frac{16}{3},2\sqrt{2}+4]$,即$S∈(\frac{16}{3},2\sqrt{2}+4]$,
∴面积S的取值范围是$(\frac{16}{3},2\sqrt{2}+4]$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、弦长公式、三角形的面积计算公式、利用导数研究函数的单调性、基本不等式的性质,考查了推理能力与计算能力,属于难题.

| A. | $\frac{139}{234}$ | B. | $\frac{134}{198}$ | C. | $\frac{175}{264}$ | D. | $\frac{28}{93}$ |
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
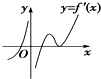
 设函数f(x)在定义域内可导且其图象如图①所示,则导函数y=f′(x)的图象最有可能是( )
设函数f(x)在定义域内可导且其图象如图①所示,则导函数y=f′(x)的图象最有可能是( )