题目内容
13.已知函数f(x)=$\frac{2b}{{a}^{x}-1}$+b+6,其中,a,b为常数,a>1,b≠0,若f(lglog210)=8,则f(lglg2)的值为( )| A. | 8 | B. | 4 | C. | -8 | D. | -4 |
分析 函数f(x)=$\frac{2b}{{a}^{x}-1}$+b+6,可得f(x)+f(-x)=$\frac{2b}{{a}^{x}-1}$+b+6+$\frac{2b}{{a}^{-x}-1}$+b+6=12,再利用对数的运算性质即可得出.
解答 解:∵函数f(x)=$\frac{2b}{{a}^{x}-1}$+b+6,
∴f(x)+f(-x)=$\frac{2b}{{a}^{x}-1}$+b+6+$\frac{2b}{{a}^{-x}-1}$+b+6=12,
而lg(log210)+lg(lg2)=$lg(lo{g}_{2}10×\frac{1}{lo{g}_{2}10})$=0,
∴f(lglog210)+f(lglg2)=12,
∴f(lglg2)=12-8=4.
故选:B.
点评 本题考查了指数函数与对数函数的运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.已知A,B,C是圆O上的三点,若$\overline{AO}$=$\frac{1}{2}$($\overline{AB}$$+\overline{AC}$),则$\overline{AB}$与$\overline{AC}$的夹角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 90° |
3.一个几何体的三视图如图所示,那么这个几何体的体积为( )
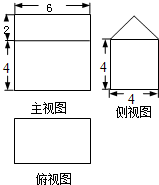

| A. | 96 | B. | 120 | C. | 144 | D. | 180 |
