Question

4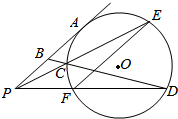．如图，过点P作⊙O的切线PA，A为切点，过PA中点B作割线交⊙O于C、D，连结PC并延长⊙O于E，连结PD，交⊙O于F，求证：EF∥PA．

Answer 1

分析 由切割线定理得：BA²=BC•BD，利用B是PA的中点，可得BP²=BC•BD，从而△PBD∽△CBP，可得∠BPC=∠PDB=∠FEC，即可得出结论．

解答 证明：由切割线定理得：BA²=BC•BD，
∵BA=PB，∴BP²=BC•BD
∴△PBD∽△CBP．
∴∠BPC=∠PDB=∠FEC，
∴EF∥PA．

点评 本题考查切割线定理，三角形相似的判定与性质，考查相似分析解决问题的能力，属于中档题．