题目内容
9.已知a>0,b>0,求证:($\frac{{a}^{2}}{b}$)${\;}^{\frac{1}{2}}$+($\frac{{b}^{2}}{a}$)${\;}^{\frac{1}{2}}$≥a${\;}^{\frac{1}{2}}$+b${\;}^{\frac{1}{2}}$.分析 通过作差、整理可知($\frac{{a}^{2}}{b}$)${\;}^{\frac{1}{2}}$+($\frac{{b}^{2}}{a}$)${\;}^{\frac{1}{2}}$-(a${\;}^{\frac{1}{2}}$+b${\;}^{\frac{1}{2}}$)=$\frac{(a-b)(\sqrt{a}-\sqrt{b})}{\sqrt{ab}}$,利用a>0、b>0可知a-b>0、$\sqrt{a}-\sqrt{b}$>0,进而计算可得结论.
解答 证明:($\frac{{a}^{2}}{b}$)${\;}^{\frac{1}{2}}$+($\frac{{b}^{2}}{a}$)${\;}^{\frac{1}{2}}$-(a${\;}^{\frac{1}{2}}$+b${\;}^{\frac{1}{2}}$)
=$\frac{a}{\sqrt{b}}$+$\frac{b}{\sqrt{a}}$-($\sqrt{a}$+$\sqrt{b}$)
=$\frac{a\sqrt{a}+b\sqrt{b}}{\sqrt{ab}}$-($\sqrt{a}$+$\sqrt{b}$)
=$\frac{a\sqrt{a}+b\sqrt{b}-a\sqrt{b}-b\sqrt{a}}{\sqrt{ab}}$
=$\frac{a(\sqrt{a}-\sqrt{b})+b(\sqrt{b}-\sqrt{a})}{\sqrt{ab}}$
=$\frac{(a-b)(\sqrt{a}-\sqrt{b})}{\sqrt{ab}}$,
又∵a>0、b>0,
∴a-b>0、$\sqrt{a}-\sqrt{b}$>0,
∴$\frac{(a-b)(\sqrt{a}-\sqrt{b})}{\sqrt{ab}}$>0,
∴($\frac{{a}^{2}}{b}$)${\;}^{\frac{1}{2}}$+($\frac{{b}^{2}}{a}$)${\;}^{\frac{1}{2}}$≥a${\;}^{\frac{1}{2}}$+b${\;}^{\frac{1}{2}}$.
点评 本题考查不等式的证明,利用作商法是解决本题的关键,注意解题方法的积累,属于中档题.

 全优点练单元计划系列答案
全优点练单元计划系列答案| A. | 0 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{4}$ |
| A. | $\frac{3\sqrt{3}}{8}$ | B. | $\frac{9\sqrt{3}}{16}$ | C. | $\frac{9\sqrt{3}}{8}$ | D. | $\frac{9\sqrt{3}}{4}$ |
| A. | ${C}_{4}^{3}$ | B. | ${P}_{4}^{3}$ | C. | ${4}_{\;}^{3}$ | D. | 34 |
| A. | $\frac{\sqrt{2}}{6}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{3}}{4}$ |
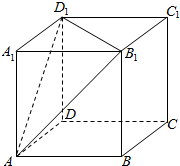 如图所示,正方体ABCD-A1B1C1D1的棱长为6,则以正方体ABCD-A1B1C1D1的中心为顶点,以平面AB1D1截正方体外接球所得的圆为底面的圆锥的全面积为$24π+18\sqrt{2}π$.
如图所示,正方体ABCD-A1B1C1D1的棱长为6,则以正方体ABCD-A1B1C1D1的中心为顶点,以平面AB1D1截正方体外接球所得的圆为底面的圆锥的全面积为$24π+18\sqrt{2}π$. 如图是一个半圆柱与多面体ABB1A1C构成的几何体,平面ABC与半圆柱的下底面共面,且AC⊥BC,P为$\widehat{{A}_{1}{B}_{1}}$上的动点.
如图是一个半圆柱与多面体ABB1A1C构成的几何体,平面ABC与半圆柱的下底面共面,且AC⊥BC,P为$\widehat{{A}_{1}{B}_{1}}$上的动点. 如图,过点P作⊙O的切线PA,A为切点,过PA中点B作割线交⊙O于C、D,连结PC并延长⊙O于E,连结PD,交⊙O于F,求证:EF∥PA.
如图,过点P作⊙O的切线PA,A为切点,过PA中点B作割线交⊙O于C、D,连结PC并延长⊙O于E,连结PD,交⊙O于F,求证:EF∥PA.