题目内容
15.为迎接2016年到来,某手工作坊的师傅要制作一种“新年礼品”,制作此礼品的次品率P与日产量x(件)满足P=$\left\{\begin{array}{l}{\frac{1}{20-x}}&{(0<x≤c)}\\{\frac{4}{5}}&{(x>c)}\end{array}\right.$(c为常数,且c∈N*,c<20),且每制作一件正品盈利4元,每出现一件次品亏损1元.(Ⅰ)将日盈利额y(元)表示为日产量x(件)的函数;
(Ⅱ)为使日盈利额最大,日制作量应为多少件?(注:次品率=$\frac{次品数}{产品总数}$×100%)
分析 (Ⅰ)通过y=(4-5P)x,分类讨论即得结论;
(Ⅱ)利用(I)可知要使日盈利额最大,则0<x≤c,通过求导可知y′=0得x=15,分0<c<15、15≤c<20两种情况讨论即可.
解答 解:(Ⅰ)依题意,y=4(x-Px)-Px=(4-5P)x,
当0<x≤c时,y=(4-$\frac{5}{20-x}$)x=$\frac{75-4x}{20-x}$x,
当x>c时,y=(4-5•$\frac{4}{5}$)x=0,
∴y=$\left\{\begin{array}{l}{\frac{-4{x}^{2}+75x}{20-x},}&{0<x≤c}\\{0,}&{x>c}\end{array}\right.$;
(Ⅱ)由(I)可知要使日盈利额最大,则0<x≤c,
此时令y′=$\frac{4(x-15)(x-25)}{(20-x)^{2}}$=0,
解得:x=15或x=25(舍),
∴当0<c<15时,y′>0,
此时y在区间(0,c]上单调递增,
∴ymax=f(c)=$\frac{-4{c}^{2}+75c}{20-c}$,此时x=c;
当15≤c<20时,y在区间(0,15)上单调递增、在区间(15,20)上单调递减,
∴ymax=f(15)=45;
综上所述,若0<c<15,则当日制作量为c件时,日盈利额最大;
若15≤c<20,则当日制作量为15件时,日盈利额最大.
点评 本题考查根据实际问题选择函数类型,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
5.设函数f(x)在R上存在导数f′(x),在(0,+∞)上f′(x)<sin2x,且?x∈R,有f(-x)+f(x)=2sin2x,则以下大小关系一定不正确的是( )
| A. | $f({-\frac{π}{6}})<f({-\frac{2π}{3}})$ | B. | $f({\frac{π}{4}})<f(π)$ | C. | $f({\frac{π}{6}})<f({\frac{2π}{3}})$ | D. | $f({-\frac{π}{4}})<f({-π})$ |
10.在△ABC中,若3cos(A-B)+5cosC=0,则tanC的最大值为( )
| A. | -$\frac{3}{4}$ | B. | -$\frac{4}{3}$ | C. | -$\frac{\sqrt{2}}{4}$ | D. | -2$\sqrt{2}$ |
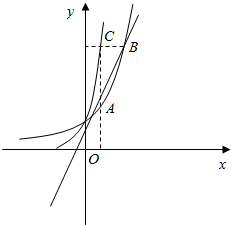 如图,在平面直角坐标系xOy中,过原点O的直线与函数y=3x的图象交于A,B两点,过B作y轴的垂线交函数y=9x的图象于点C,若AC平行于y轴,则点A的坐标是(log32,2).
如图,在平面直角坐标系xOy中,过原点O的直线与函数y=3x的图象交于A,B两点,过B作y轴的垂线交函数y=9x的图象于点C,若AC平行于y轴,则点A的坐标是(log32,2).