题目内容
3．不论a取何值，函数f（x）=ax-1-1（a＞0且a≠1）的图象恒过定点为（1，0）．分析 根据指数函数y=ax的图象恒过定点（0，1），即可求出函数f（x）=ax-1-1的图象恒过定点的坐标．
解答 解：当x-1=0，即x=1时，
y=f（x）=a0-1=1-1=0，
∴函数f（x）=ax-1-1的图象恒过定点（1，0）．
故答案为：（1，0）．
点评 本题考查了指数函数的图象与性质的应用问题，是基础题目．
练习册系列答案
名校课堂系列答案
相关题目
11．由曲线y=$\sqrt{x}$、直线y=-x+2及x轴所围成的图形的面积为（ ）
| A． | $\frac{10}{3}$ | B． | 4 | C． | $\frac{7}{6}$ | D． | 6 |
8．
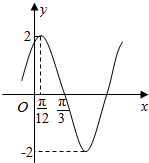已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，为了解函数g（x）=Asin（ωx）的图象，只要将y=f（x）的图象（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，为了解函数g（x）=Asin（ωx）的图象，只要将y=f（x）的图象（ ）| A． | 向左平移$\frac{π}{3}$个单位长度 | B． | 向右平移$\frac{π}{3}$个单位长度 | ||
| C． | 向左平移$\frac{π}{6}$个单位长度 | D． | 向右平移$\frac{π}{6}$个单位长度 |