题目内容
20.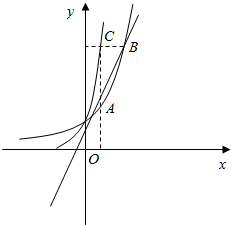 如图,在平面直角坐标系xOy中,过原点O的直线与函数y=3x的图象交于A,B两点,过B作y轴的垂线交函数y=9x的图象于点C,若AC平行于y轴,则点A的坐标是(log32,2).
如图,在平面直角坐标系xOy中,过原点O的直线与函数y=3x的图象交于A,B两点,过B作y轴的垂线交函数y=9x的图象于点C,若AC平行于y轴,则点A的坐标是(log32,2).
分析 设A(n,3n),B(m,3m),由图象和解析式求出点C的坐标,根据A,B,O三点共线,利用斜率相等、指数、对数的运算求得点A的坐标.
解答 解:由题意设A(n,3n),B(m,3m),
由9x=3m=32x,即m=2x,解得x=$\frac{m}{2}$,则C($\frac{m}{2}$,3m),
∵AC平行于y轴,∴n=$\frac{m}{2}$,则m=2n,
∴A($\frac{m}{2}$,3n),B(m,3m),
又A,B,O三点共线,∴kOA=kOB,
则$\frac{{3}^{n}}{\frac{m}{2}}=\frac{{3}^{m}}{m}$,∴3m=2•3n=32n,
得3n=2,即n=log32,且${3}^{n}={3}^{lo{g}_{3}^{2}}$=2,
∴点A的坐标是(log32,2).
故答案为:(log32,2).
点评 本题考查指数函数的图象与性质,指数、对数的运算,直线的斜率公式、三点共线的判定方法等,综合性较强,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
10.位于西部地区的A,B两地,据多年的资料记载:A,B两地一年中下雨天仅占6%和8%,而同时下雨的比例为2%,则A地为雨天时,B地也为雨天的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 0.12 | D. | 0.18 |
11.由曲线y=$\sqrt{x}$、直线y=-x+2及x轴所围成的图形的面积为( )
| A. | $\frac{10}{3}$ | B. | 4 | C. | $\frac{7}{6}$ | D. | 6 |
8.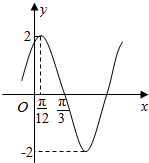 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了解函数g(x)=Asin(ωx)的图象,只要将y=f(x)的图象( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了解函数g(x)=Asin(ωx)的图象,只要将y=f(x)的图象( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了解函数g(x)=Asin(ωx)的图象,只要将y=f(x)的图象( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了解函数g(x)=Asin(ωx)的图象,只要将y=f(x)的图象( )| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
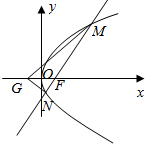 已知点F是抛物线C:y2=2px(p>0)的焦点,点A(m,2)在抛物线C上,且AF=2
已知点F是抛物线C:y2=2px(p>0)的焦点,点A(m,2)在抛物线C上,且AF=2