题目内容
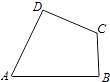
【题目】如图，某广场中间有一块边长为2百米的菱形状绿化区ABCD，其中BMN是半径为1百米的扇形，∠ABC= 
．管理部门欲在该地从M到D修建小路：在 
上选一点P（异于M，N两点），过点P修建与BC平行的小路PQ．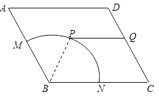 
（1）若∠PBC= 
，求PQ的长度；
（2）当点P选择在何处时，才能使得修建的小路 
与PQ及QD的总长最小？并说明理由．
【答案】
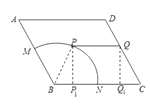
（1）解．如图示：
，
连接BP，过P作PP1⊥BC，垂足为P1，过Q作QQ1⊥BC垂足为Q1，
在Rt△PBP1中， 
，PQ=1
（2）解．设∠PBP1=θ， 
，
∴ 
，
在Rt△QBQ1中， 
，
∴总路径长f（θ）= 
﹣θ+4﹣cosθ﹣ 
sinθ，（0＜θ＜ ），
f′（θ）=sinθ﹣ cosθ﹣1=2sin（θ﹣ 
）﹣1，
令f'（θ）=0， 
，
当 
时，f'（θ）＜0，
当 
时，f'（θ）＞0，
所以当 时，总路径最短．
答：当BP⊥BC时，总路径最短
【解析】（1）作出辅助线，根据梯形的性质求出PQ的长即可；（2）设∠PBP1=θ，求出PQ的长，得到总路径长f（θ）的表达式，通过求导得到函数的单调性，从而求出去最小值时θ的值，即P点的位置即可．
练习册系列答案
相关题目
