题目内容
【题目】如图，A，B，C，D为平面四边形ABCD的四个内角．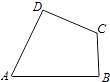 
（1）证明：tan 
= 
；
（2）若A+C=180°，AB=6，BC=3，CD=4，AD=5，求tan +tan 
+tan 
+tan 
的值．
【答案】
（1）证明： tan 
= 
= 
= 
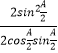．等式成立．
（2）解：由A+C=180°，得C=180°﹣A，D=180°﹣B，由（Ⅰ）可知：tan +tan 
+tan 
+tan 
= 
= 
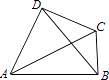
，连结BD，在△ABD中，有BD2=AB2+AD2﹣2ABADcosA，AB=6，BC=3，CD=4，AD=5，
在△BCD中，有BD2=BC2+CD2﹣2BCCDcosC，
所以AB2+AD2﹣2ABADcosA=BC2+CD2﹣2BCCDcosC，
则：cosA= 
= 
= 
．
于是sinA= 
= 
，
连结AC，同理可得：cosB= 
= 
= 
，
于是sinB= 
= 
．
所以tan +tan +tan +tan = = 
= 
．
【解析】（1）直接利用切化弦以及二倍角公式化简证明即可．（2）通过A+C=180°，得C=180°﹣A，D=180°﹣B，利用（1）化简tan +tan +tan +tan = ，连结BD，在△ABD中，利用余弦定理求出sinA，连结AC，求出sinB，然后求解即可．
全能闯关100分系列答案
【题目】某保险的基本保费为a（单位：元），继续购买该保险的投保人成为续保人，续保人本年度的保费与其上年度出险次数的关联如下：
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
设该险种一续保人一年内出险次数与相应概率如下：
一年内出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
（1）求一续保人本年度的保费高于基本保费的概率；
（2）若一续保人本年度的保费高于基本保费，求其保费比基本保费高出60%的概率；
（3）求续保人本年度的平均保费与基本保费的比值．
