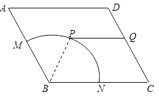
题目内容
【题目】设![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点.
的左、右焦点.
(1)若![]() 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求![]() 的最大值和最小值;
的最大值和最小值;
(2)设过定点![]() 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点![]() 、
、![]() ,且
,且![]() 为锐角(其中
为锐角(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
【答案】(1)最小值-2,最大值1;(2)![]() 或
或![]() .
.
【解析】
(1)由椭圆方程求出焦点坐标,![]() 是第一象限内该椭圆上的一点设为
是第一象限内该椭圆上的一点设为![]() ,利用
,利用![]() ,结合
,结合![]() 在椭圆上,可求
在椭圆上,可求![]() 的最大值和最小值;(2)设直线
的最大值和最小值;(2)设直线![]() ,与椭圆方程联立,整理得
,与椭圆方程联立,整理得![]() ,利用韦达定理以及平面向量数量积公式,可得
,利用韦达定理以及平面向量数量积公式,可得![]() ,结合判别式大于零可求直线
,结合判别式大于零可求直线![]() 的斜率
的斜率![]() 取值范围.
取值范围.
由椭圆![]() 知
知![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() .设
.设![]() ,则
,则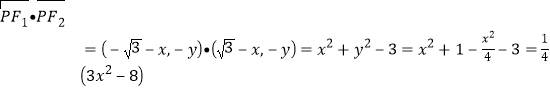 ,
,
因为![]() ,故当
,故当![]() ,即点
,即点![]() 为椭圆短轴端点时,
为椭圆短轴端点时,![]() 有最小值-2.
有最小值-2.
当![]() ,即点
,即点![]() 为椭圆长轴端点时,
为椭圆长轴端点时,![]() 有最大值1.
有最大值1.
(2)显然直线![]() 不满足题设条件,可设直线
不满足题设条件,可设直线![]() ,
,![]() ,
,![]() ,
,
联立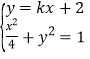 消去
消去![]() ,整理得
,整理得![]() .
.
![]() ,
,![]() .由
.由![]() ,
,
得![]() 或
或![]() .①
.①
又![]() ,
,![]() .
.
又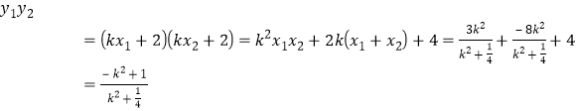 ,
,
![]() ,即
,即![]() .
.![]() .②
.②
故由①②得![]() 或
或![]() .
.

【题目】从某山区养殖场散养的3500头猪中随机抽取5头,测量猪的体长x(cm)和体重y(kg),得如下测量数据:
猪编号 | 1 | 2 | 3 | 4 | 5 |
x | 169 | 181 | 166 | 185 | 180 |
y | 95 | 100 | 97 | 103 | 101 |
(1)当且仅当x,y满足:x≥180且y≥100时,该猪为优等品,用上述样本数据估计山区养殖场散养的3500头猪中优等品的数量;
(2)从抽取的上述5头猪中,随机抽取2头中优等品数x的分布列及其数学期望.
【题目】某保险的基本保费为a(单位:元),继续购买该保险的投保人成为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
设该险种一续保人一年内出险次数与相应概率如下:
一年内出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
(1)求一续保人本年度的保费高于基本保费的概率;
(2)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;
(3)求续保人本年度的平均保费与基本保费的比值.