题目内容
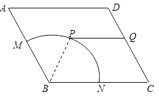
【题目】如图,已知四边形![]() 是边长为1的正方形,点
是边长为1的正方形,点![]() 、
、![]() 、
、![]() 、
、![]() 顺次在边
顺次在边![]() 、
、![]() 、
、![]() 、
、![]() 上,且
上,且![]() .过点
.过点![]() 、
、![]() 、
、![]() 、
、![]() 分别作射线
分别作射线![]() 、
、![]() 、
、![]() 、
、![]() ,且
,且![]() ,这里
,这里![]() 为定角,且
为定角,且![]() ,由此得到四边形
,由此得到四边形![]() .
.

(1)问四边形![]() 是怎样的四边形?证明你的结论.
是怎样的四边形?证明你的结论.
(2)设![]() ,试将
,试将![]() 表示成
表示成![]() 的函数.
的函数.
(3)是否存在![]() ,使
,使![]() 为与
为与![]() 无关的定值?若存在,求出相应的
无关的定值?若存在,求出相应的![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1) 正方形(2) ![]() ,其中,
,其中,![]() .(3)
.(3) ![]()
【解析】
(1)四边形![]() 为正方形.
为正方形.
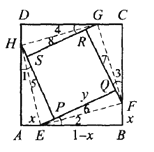
如图,联结![]() 、
、![]() 、
、![]() 、
、![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() .则
.则![]() .
.
于是,![]() .进而,
.进而,![]() .
.
又由题设可知![]() .故
.故![]() .
.
但![]() ,则
,则![]() .
.
同理,![]() .
.
故,![]() ,
,![]() ,
,![]() .
.
从而,![]() .
.
(2)设![]() ,则
,则
![]()
![]()
![]() ,
,
即![]() .
.
同理,计算![]() 可得
可得![]() .
.
相减得![]() ,其中,
,其中,![]() .
.
另解:将折线EQF分别投影到AB、![]() 上,得
上,得
![]()
即![]()
消去![]() 即得
即得![]() .
.
(3)![]() .
.
欲使![]() 是与
是与![]() 无关的常数,必须且只须
无关的常数,必须且只须![]() ,即
,即![]() .
.
因此,当![]() 时,
时,![]() 是与
是与![]() 无关的常数.
无关的常数.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目