题目内容
已知抛物线C:x2=2py(p>0)的焦点F在直线l:x-y+1=0上
(I)求抛物线C的方程;
(Ⅱ)设直线l与抛物线C相交于P,Q两点,求线段PQ中点M的坐标.
(I)求抛物线C的方程;
(Ⅱ)设直线l与抛物线C相交于P,Q两点,求线段PQ中点M的坐标.
(I)∵抛物线C:x2=2py(p>0)的焦点为F(0,
p)
∴0-
p+1=0,可得p=2,
因此抛物线C的方程是x2=4y;
(II)由
,消去y得
x2-x-1=0
设P(x1,y1),Q(x2,y2)
∴x1+x2=4,可得中点M的横坐标为
=2(x1+x2)=2
代入直线l方程,得纵坐标为yM=xM+1=3
即线段PQ中点M的坐标(2,3).
| 1 |
| 2 |
∴0-
| 1 |
| 2 |
因此抛物线C的方程是x2=4y;
(II)由
|
| 1 |
| 4 |
设P(x1,y1),Q(x2,y2)
∴x1+x2=4,可得中点M的横坐标为
| 1 |
| 2 |
代入直线l方程,得纵坐标为yM=xM+1=3
即线段PQ中点M的坐标(2,3).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
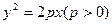 的焦点,与抛物线交于两点A、B将直线AB接向量
的焦点,与抛物线交于两点A、B将直线AB接向量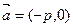 平移得直线
平移得直线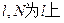 的动点,M为抛物线弧AB上的动点
的动点,M为抛物线弧AB上的动点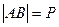 ,求抛物线方程
,求抛物线方程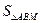 的最大值
的最大值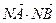 的最小值
的最小值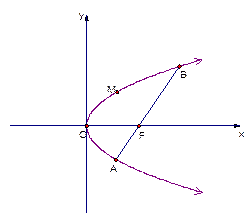
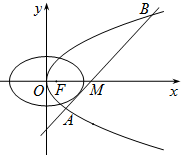
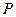 在抛物线
在抛物线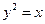 上,点
上,点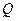 在圆
在圆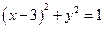 上,求
上,求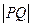 的最小值。
的最小值。