题目内容
【题目】已知函数![]() .
.
(Ⅰ)若![]() ,证明:函数
,证明:函数![]() 在
在![]() 上单调递减;
上单调递减;
(Ⅱ)是否存在实数![]() ,使得函数
,使得函数![]() 在
在![]() 内存在两个极值点?若存在,求实数
内存在两个极值点?若存在,求实数![]() 的取值范围;若不存在,请说明理由. (参考数据:
的取值范围;若不存在,请说明理由. (参考数据: ![]() ,
, ![]() )
)
【答案】(Ⅰ)证明见解析;(Ⅱ) 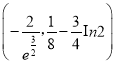 .
.
【解析】试题分析:(I);求导得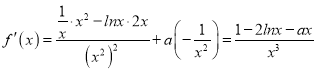 ,只需利用导数研究函数
,只需利用导数研究函数![]() 的单调性,求出最大值,从而证明
的单调性,求出最大值,从而证明![]() 即可得结论;(II)讨论
即可得结论;(II)讨论![]() 时,
时, ![]() 时两种情况,分别利用导数研究函数的单调性,排除不合题意的情况,从而可得使得函数
时两种情况,分别利用导数研究函数的单调性,排除不合题意的情况,从而可得使得函数![]() 在
在![]() 内存在两个极值点的实数
内存在两个极值点的实数![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)函数![]() 的定义域是
的定义域是![]() .
.
求导得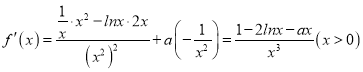 .
.
设![]() ,则
,则![]() 与
与![]() 同号.
同号.
所以![]() ,若
,若![]() ,则
,则![]() 对任意
对任意![]() 恒成立.
恒成立.
所以函数![]() 在
在![]() 上单调递减.
上单调递减.
又![]() ,
,
所以当![]() 时,满足
时,满足![]() .即当
.即当![]() 时,满足
时,满足![]() .
.
所以函数![]() 在
在![]() 上单调递减.
上单调递减.
(Ⅱ)①当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减.
上单调递减.
由![]() ,又
,又![]() ,
, ![]() 时,
时, ![]() ,
,
取![]() ,则
,则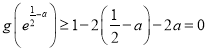 ,
,
所以一定存在某个实数![]() ,使得
,使得![]() .
.
故在![]() 上,
上, ![]() ;在
;在![]() 上,
上, ![]() .
.
即在![]() 上,
上, ![]() ;在
;在![]() 上,
上, ![]() .
.
所以函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.此时函数
上单调递减.此时函数![]() 只有1个极值点
只有1个极值点![]() ,不合题意,舍去;
,不合题意,舍去;
②当![]() 时,令
时,令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() ,
,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
故函数![]() 的单调情况如下表:
的单调情况如下表:
|
|
|
|
|
| 0 | + |
|
| 极小值 |
|
要使函数![]() 在
在![]() 内存在两个极值点,则需满足
内存在两个极值点,则需满足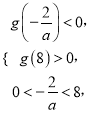 ,即
,即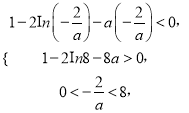 ,
,
解得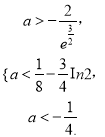 又
又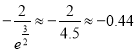 ,
, ![]() ,
,
所以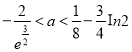 .
.
此时, ![]() ,
,
又 ,
, 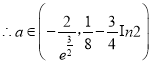 ;
;
综上,存在实数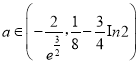 ,使得函数
,使得函数![]() 在
在![]() 内存在两个极值点.
内存在两个极值点.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目