题目内容
【题目】已知向量
，
， 
（1）求函数
的最小正周期及
取得最大值时对应的x的值；
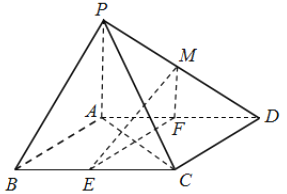
（2）在锐角三角形ABC中，角A、B、C的对边为a、b、c，若
,求三角形ABC面积的最大值并说明此时该三角形的形状.
【答案】(1)最小正周期为π，最大值为
， 
(2) 
，等边三角形
【解析】试题分析：（1）先利用诱导公式化简
的坐标，再利用平面向量的数量积、二倍角公式及配角公式化简表达式 ，再利用三角函数的性质进行求解；（2）先利用
求出角
，再利用余弦公式、基本不等式和三角形的面积公式进行求解.
试题解析：（1）由已知得
，又
于是
∴ 
的最小正周期为
；
当
，即
，的最大值为
.
（2）锐角三角形
中，由（1）得
∴ 
，∴
由余弦定理知
∴
即
(当且仅当
时取得等号成立) ∴
,
∴当三角形为等边三角形时面积取得最大值为
.
【题目】心理学家分析发现视觉和空间能力与性别有关，某数学兴趣小组为了验证这个结论，从兴趣小组中按分层抽样的方法抽取50名同学（男30女20），给所有同学几何题和代数题各一题，让各位同学自由选择一道题进行解答．选题情况如下表：（单位：人）
几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
（Ⅰ）能否据此判断有97．5%的把握认为视觉和空军能力与性别有关？
（Ⅱ）经过多次测试后，甲每次解答一道几何题所用的时间在5—7分钟，乙每次解答一道几何题所用的时间在6—8分钟，现甲、乙各解同一道几何题，求乙比甲先解答完的概率．
（Ⅲ）现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究，记甲、乙两女生被抽到的人数为
，求的分布列及数学期望
．
附表及公式
| 0．15 | 0．10 | 0．05 | 0．025 | 0．010 | 0．005 | 0．001 |
| 2．072 | 2．706 | 3．841 | 5．024 | 6．635 | 7．879 | 10．828 |
【题目】某企业有甲、乙两套设备生产同一种产品，为了检测两套设备的生产质量情况，随机从两套设备生产的大量产品中各抽取了50件产品作为样本，检测一项质量指标值，若该项质量指标值落在
内，则为合格品，否则为不合格品. 表1是甲套设备的样本的频数分布表，图1是乙套设备的样本的频率分布直方图.
表1：甲套设备的样本的频数分布表
质量指标值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
频数 | 1 | 5 | 18 | 19 | 6 | 1 |
图1：乙套设备的样本的频率分布直方图
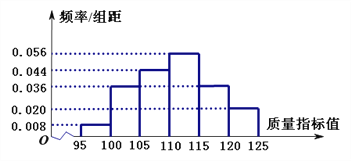
（Ⅰ）将频率视为概率. 若乙套设备生产了5000件产品，则其中的不合格品约有多少件；
（Ⅱ）填写下面列联表，并根据列联表判断是否有90%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关；
甲套设备 | 乙套设备 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
（Ⅲ）根据表1和图1，对两套设备的优劣进行比较.
附：
.
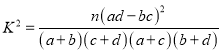