题目内容
【题目】某校教务处对学生学习的情况进行调研,其中一项是:对“学习数学”的态度是否与性别有关,可见随机抽取了30名学生进行了问卷调查,得到了如下联表:
男生 | 女生 | 合计 | |
喜欢 | 10 | ||
不喜欢 | 8 | ||
合计 | 30 |
已知在这30人中随机抽取1人,抽到喜欢“学习数学”的学生的概率是![]() .
.
(1)请将上面的列联表补充完整(在答题卷上直接填写结果,不需要写求解过程);
(2)若从喜欢“学习数学”的女生中抽取2人进行调研,其中女生甲被抽到的概率为多少?(要写求解过程)
(3)试判断是否有95%的把握认为喜欢“学习数学”与性别有关?
附: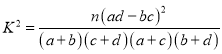 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(1)见解析;(2) ![]() (3) 没有95%的把握认为喜欢“学习数学”与性别有关.
(3) 没有95%的把握认为喜欢“学习数学”与性别有关.
【解析】
(1)由条件可得喜欢学数学的人数为![]() ,可根据已知喜欢学数学的男生的人数为10,算出喜欢学数学的女生人数6,从而再算出不喜欢学数学的人数,又由于已知不喜欢学数学女生的人数为8,从而算出不喜欢学数学男生的人数为6.最后填完表格;(2)算出抽到没有抽到甲的概率,再算出抽到甲的概率;(3)用公式代入和图标中数据进行比较。
,可根据已知喜欢学数学的男生的人数为10,算出喜欢学数学的女生人数6,从而再算出不喜欢学数学的人数,又由于已知不喜欢学数学女生的人数为8,从而算出不喜欢学数学男生的人数为6.最后填完表格;(2)算出抽到没有抽到甲的概率,再算出抽到甲的概率;(3)用公式代入和图标中数据进行比较。
解:(1)抽到喜欢“学习数学”的学生人数是![]() ,补充完列联表如下:
,补充完列联表如下:
男生 | 女生 | 合计 | |
喜欢 | 10 | 6 | 16 |
不喜欢 | 6 | 8 | 14 |
合计 | 16 | 14 | 30 |
(2)由(1)知喜欢“学习数学”的女生有6人,
记其他5位女生分别为A、B、C、D、E,如果抽取两人中没有甲,则是在A、B、C、D、E五人中选取两人,一共![]() 种可能。总取法一共
种可能。总取法一共![]() 种可能。
种可能。
故所求的概率为![]() ;
;
(3)设![]() :喜欢“学习数学”与性别是否有关;
:喜欢“学习数学”与性别是否有关;
由已知数据得,![]() ,
,
所以没有95%的把握认为喜欢“学习数学”与性别有关.

 阅读快车系列答案
阅读快车系列答案【题目】为了研究高二阶段男生、女生对数学学科学习的差异性,在高二年级所有学生中随机抽取25名男生和25名女生,计算他们高二上学期期中、期末和下学期期中、期末的四次数学考试成绩的各自的平均分,并绘制成如图所示的茎叶图.
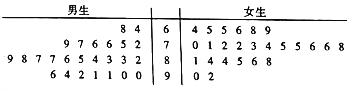
(1)请根据茎叶图判断,男生组与女生组哪组学生的数学成绩较好?请用数据证明你的判断;
(2)以样本中50名同学数学成绩的平均分x0(79.68分)为分界点,将各类人数填入如下的列联表:
分数 性别 | 高于或等于x0 | 低于x0 | 合计 |
男生 | |||
女生 | |||
合计 |
(3)请根据(2)中的列联表,判断能否有99%的把握认为数学学科学习能力与性别有关?
附:K2=![]()
P(K2≥k0) | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |