题目内容
【题目】曲线
是平面内到直线
和直线
的距离之积等于常数
（
）的点的轨迹，下列四个结论：
①曲线过点
；
②曲线关于点成中心对称；
③若点
在曲线上，点
、
分别在直线
、
上，则
不小于
；
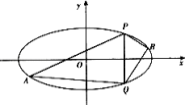
④设
为曲线上任意一点，则点关于直线，点及直线对称的点分别为
、
、
，则四边形
的面积为定值
；
其中，所有正确结论的序号是________
【答案】②③④
【解析】
由题意曲线C是平面内到直线
和直线
的距离之积等于常数
的点的轨迹，利用直接法，设动点坐标为
，可得动点的轨迹方程，然后由方程特点进行判断。
由题意设动点坐标为，则由题意及点到直线的距离公式得：
，
对于①将
代入验证可知方程不过此点，所以①错；
对于②，把方程中的
被
代换，
被
代换，方程不变，所以曲线
关于点成中心对称，②正确；
对于③，由题意知P在曲线C上，点A,B分别在直线
上，
则
，所以③正确；
对于④，由题意知点
在曲线C上，根据对称性，则四边形
的面积
，所以④正确。
故答案为：②③④
练习册系列答案
相关题目
【题目】某校教务处对学生学习的情况进行调研，其中一项是：对“学习数学”的态度是否与性别有关，可见随机抽取了30名学生进行了问卷调查，得到了如下联表：
男生 | 女生 | 合计 | |
喜欢 | 10 | ||
不喜欢 | 8 | ||
合计 | 30 |
已知在这30人中随机抽取1人，抽到喜欢“学习数学”的学生的概率是
.
（1）请将上面的列联表补充完整（在答题卷上直接填写结果，不需要写求解过程）；
（2）若从喜欢“学习数学”的女生中抽取2人进行调研，其中女生甲被抽到的概率为多少?（要写求解过程）
（3）试判断是否有95%的把握认为喜欢“学习数学”与性别有关？
附：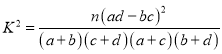
，其中
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
