题目内容
【题目】已知椭圆
，圆心为坐标原点的单位圆O在C的内部，且与C有且仅有两个公共点，直线
与C只有一个公共点.
（1）求C的标准方程；
（2）设不垂直于坐标轴的动直线l过椭圆C的左焦点F，直线l与C交于A，B两点，且弦AB的中垂线交x轴于点P，求
的值.
【答案】(1) 
(2) 
【解析】
（1）利用单位圆的性质求得
，利用直线
和椭圆联立方程后关于
的方程只有一个解，判别式为
列方程，由此求得
.进而求得椭圆的标准方程.
（2）设出直线
的方程，代入椭圆方程，写出韦达定理，求得
中点
的坐标，利用中垂线的斜率列方程，求得
点的横坐标，由此求得
.利用弦长公式求得
，进而求得
的值.
（1）依题意，得
将
代入椭圆的方程，得
由
，解得
所以椭圆的标准方程为
（2）由（1）可得左焦点
由题意设直线的方程为
，
代入椭圆方程，得
设
，则
所以
,AB的中点为
设点
，则
，
解得
所以
又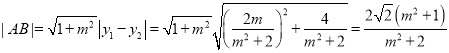
所以
【题目】学校为了了解高三学生每天自主学习中国古典文学的时间，随机抽取了高三男生和女生各50名进行问卷调查，其中每天自主学习中国古典文学的时间超过3小时的学生称为“古文迷”，否则为“非古文迷”，调查结果如表：
古文迷 | 非古文迷 | 合计 | |
男生 | 26 | 24 | 50 |
女生 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
（Ⅰ）根据表中数据能否判断有
的把握认为“古文迷”与性别有关？
（Ⅱ）现从调查的女生中按分层抽样的方法抽出5人进行调查，求所抽取的5人中“古文迷”和“非古文迷”的人数；
（Ⅲ）现从（Ⅱ）中所抽取的5人中再随机抽取3人进行调查，记这3人中“古文迷”的人数为
，求随机变量
的分布列与数学期望．
参考公式： 
，其中
．
参考数据：
| 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.321 | 3.841 | 5.024 | 6.635 |
【题目】某景区的各景点从2009年取消门票实行免费开放后，旅游的人数不断地增加，不仅带动了该市淡季的旅游，而且优化了旅游产业的结构，促进了该市旅游向“观光、休闲、会展”三轮驱动的理想结构快速转变．下表是从2009年至2018年，该景点的旅游人数
（万人）与年份
的数据：
第 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
旅游人数 | 300 | 283 | 321 | 345 | 372 | 435 | 486 | 527 | 622 | 800 |
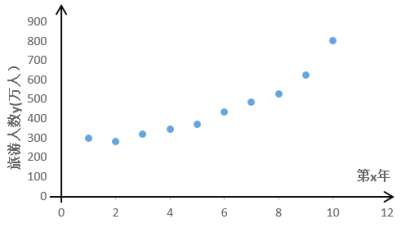
该景点为了预测2021年的旅游人数，建立了与的两个回归模型：
模型①：由最小二乘法公式求得
与的线性回归方程
；
模型②：由散点图的样本点分布，可以认为样本点集中在曲线
的附近．
（1）根据表中数据，求模型②的回归方程
．（
精确到个位，
精确到0．01）．
（2）根据下列表中的数据，比较两种模型的相关指数
，并选择拟合精度更高、更可靠的模型，预测2021年该景区的旅游人数（单位：万人，精确到个位）．
回归方程 | ① | ② |
| 30407 | 14607 |
参考公式、参考数据及说明：
①对于一组数据
，其回归直线
的斜率和截距的最小二乘法估计分别为
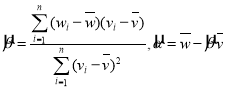．②刻画回归效果的相关指数
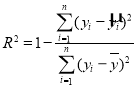；③参考数据：
，
．
|
|
|
|
|
|
5．5 | 449 | 6．05 | 83 | 4195 | 9．00 |
表中
．
【题目】某校教务处对学生学习的情况进行调研，其中一项是：对“学习数学”的态度是否与性别有关，可见随机抽取了30名学生进行了问卷调查，得到了如下联表：
男生 | 女生 | 合计 | |
喜欢 | 10 | ||
不喜欢 | 8 | ||
合计 | 30 |
已知在这30人中随机抽取1人，抽到喜欢“学习数学”的学生的概率是
.
（1）请将上面的列联表补充完整（在答题卷上直接填写结果，不需要写求解过程）；
（2）若从喜欢“学习数学”的女生中抽取2人进行调研，其中女生甲被抽到的概率为多少?（要写求解过程）
（3）试判断是否有95%的把握认为喜欢“学习数学”与性别有关？
附：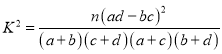
，其中
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
