题目内容
10.已知:sin230°+sin290°+sin2150°=$\frac{3}{2}$
sin25°+sin265°+sin2125°=$\frac{3}{2}$
sin218°+sin278°+sin2138°=$\frac{3}{2}$
…
通过观察上述等式的规律,写出一般性的命题:sin2(α-60°)+sin2α+sin2(α+60°)=$\frac{3}{2}$.
分析 分析已知条件中:sin230°+sin290°+sin2150°=$\frac{3}{2}$,sin25°+sin265°+sin2125°=$\frac{3}{2}$,sin218°+sin278°+sin2138°=$\frac{3}{2}$,…我们可以发现等式左边参加累加的三个均为正弦的平方,且三个角组成一个以60°为公差的等差数列,右边是常数,由此不难得到结论.
解答 解:由已知中:
sin230°+sin290°+sin2150°=$\frac{3}{2}$
sin25°+sin265°+sin2125°=$\frac{3}{2}$
sin218°+sin278°+sin2138°=$\frac{3}{2}$
…
归纳推理的一般性的命题为:sin2(α-60°)+sin2α+sin2(α+60°)=$\frac{3}{2}$.
故答案为:sin2(α-60°)+sin2α+sin2(α+60°)=$\frac{3}{2}$
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想),(3)论证.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.执行如图的程序框图,输出的s=( )
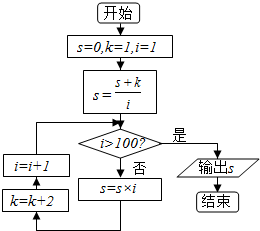

| A. | 10000 | B. | 5050 | C. | 101 | D. | 100 |