题目内容
20.求下列各式的值.(1)($\frac{9}{16}$)${\;}^{\frac{1}{2}}$+$\root{3}{1000}$-($\frac{64}{27}$)${\;}^{-\frac{1}{3}}$+3•e0;
(2)$\frac{lg\sqrt{27}+lg8-{log}_48}{\frac{1}{2}lg0.3+lg2}$;
(3)lg25+lg2•lg50.
分析 (1)利用有理指数幂的运算法则化简求解即可.
(2)(3)利用对数的运算法则化简求解即可.
解答 (本题满分12分)
解:(1)($\frac{9}{16}$)${\;}^{\frac{1}{2}}$+$\root{3}{1000}$-($\frac{64}{27}$)${\;}^{-\frac{1}{3}}$+3•e0
=$\frac{3}{4}$+10$-\frac{3}{4}$+3
=13.
(2)$\frac{lg\sqrt{27}+lg8-{log}_{4}8}{\frac{1}{2}lg0.3+lg2}$=$\frac{\frac{3}{2}lg3+3lg2-\frac{3}{2}l{og}_{2}2}{\frac{1}{2}lg\frac{3}{10}+lg2}$=3.
(3)lg25+lg2•lg50=lg25+lg$\frac{10}{5}$•lg(10×5)=lg25+(1-lg5)•(1+lg5)=1.
点评 本题考查对数的运算法则的应用,有理指数幂的化简求值,考查计算能力.

练习册系列答案
相关题目
11.在平面直角坐标系中,不等式组$\left\{\begin{array}{l}{x-1≤0}\\{x+y≥0}\\{x-y+4≥0}\end{array}\right.$,表示的平面区域的面积是( )
| A. | 3 | B. | $\frac{9}{2}$ | C. | 6 | D. | 9 |
8.为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查,就是否“取消英语听力”的问题,调查统计的结果如下表:
已知在全体样本中随机抽取1人,抽到持“应该保留”态度的人的概率为0.05.
(1)现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数ξ的分布列和数学期望.
| 应该取消 | 应该保留 | 无所谓 | |
| 在校学生 | 2100人 | 120人 | y人 |
| 社会人士 | 600人 | x人 | z人 |
(1)现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数ξ的分布列和数学期望.

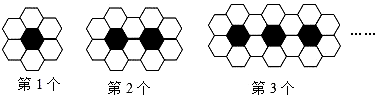
 用黑白两种正六边形瓷砖按如图所示规律拼成若干图案.
用黑白两种正六边形瓷砖按如图所示规律拼成若干图案.