题目内容
2.已知A(0,0),B(1,0),C(2,1),D(0,3),将四边形ABCD绕y轴旋转一周,求所得旋转体的表面积和体积.分析 过C作y轴的垂线交y轴于E,则三角形DCE是直角三角形,四边形ABCE是直角梯形,进而可得四边形ABCD绕y轴旋转一周所得几何体是一个圆锥和一个圆台的组合体,结合圆台和圆锥的表面积体积公式,可得答案.
解答 解:过C作y轴的垂线交y轴于E,则三角形DCE是直角三角形,四边形ABCE是直角梯形,
四边形ABCD绕y轴旋转一周所得几何体是一个圆锥和一个圆台的组合体,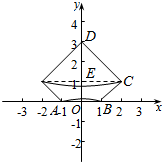
易求得$AB=1,BC=\sqrt{2},CD=2,AE=1,ED=2,DC=2\sqrt{2}$----------(6分)
所得旋转体的表面积是S=$π×{1^2}+π(1+2)×\sqrt{2}+π×2×2\sqrt{2}=(7\sqrt{2}+1)π$,-----(9分)
体积为V=$\frac{1}{3}×π×4×2+\frac{π}{3}(1+2+4)×1=5π$.-----------------(12分)
点评 本题考查的知识点是旋转体,熟练掌握圆台和圆锥的体积和表面积公式是解答的关键

练习册系列答案
相关题目
13.直线xcos140°+ysin140°-2=0的倾斜角是( )
| A. | 40° | B. | 50° | C. | 130° | D. | 140° |
17.复数(1+i)z=1-2i的虚部是( )
| A. | $-\frac{3}{2}$ | B. | $-\frac{1}{2}$ | C. | $-\frac{3}{2}i$ | D. | $-\frac{1}{2}i$ |
