题目内容
18.直线l过点A(3,2)与圆x2+y2-4x+3=0相切,则直线l的方程为x=3或3x-4y-1=0.分析 根据直线和圆相切的条件进行求解即可.
解答 解:圆的标准方程为(x-2)2+y2=1,
则圆心坐标为(2,0),半径R=1
若直线斜率k不存在,则直线方程为x=3,圆心到直线的距离d=3-2=1,满足条件.
若直线斜率k存在,则直线方程为y-2=k(x-3),
即kx-y+2-3k=0,
圆心到直线的距离d=$\frac{|2-k|}{\sqrt{{k}^{2}+1}}$=1,平方得k=$\frac{3}{4}$,此时切线方程为3x-4y-1=0,
综上切线方程为x=3或3x-4y-1=0,
故答案为:x=3或3x-4y-1=0.
点评 本题主要考查直线和圆的位置关系的应用,根据直线和圆相切的等价条件是解决本题的关键.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
13.直线xcos140°+ysin140°-2=0的倾斜角是( )
| A. | 40° | B. | 50° | C. | 130° | D. | 140° |
8.为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查,就是否“取消英语听力”的问题,调查统计的结果如下表:
已知在全体样本中随机抽取1人,抽到持“应该保留”态度的人的概率为0.05.
(1)现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数ξ的分布列和数学期望.
| 应该取消 | 应该保留 | 无所谓 | |
| 在校学生 | 2100人 | 120人 | y人 |
| 社会人士 | 600人 | x人 | z人 |
(1)现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数ξ的分布列和数学期望.
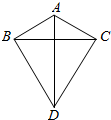 如图,在△ABC中,AB=AC=a,以BC为边向外作正三角形BCD,则AD的最大值为2a.
如图,在△ABC中,AB=AC=a,以BC为边向外作正三角形BCD,则AD的最大值为2a.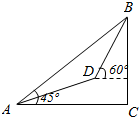 某登山队在山脚A处测得山顶B的仰角为45°,沿倾斜角为30°的斜坡前进1000m后到达D处,又测得山顶的仰角为60°,则山的高度BC为$500(\sqrt{3}+1)$m.
某登山队在山脚A处测得山顶B的仰角为45°,沿倾斜角为30°的斜坡前进1000m后到达D处,又测得山顶的仰角为60°,则山的高度BC为$500(\sqrt{3}+1)$m.