题目内容
17.若x,y满足$\left\{\begin{array}{l}{x+y-2≥0}\\{kx-y+2≥0}\\{y≥0}\end{array}\right.$,且z=y-x的最小值为-4,则k的值为$-\frac{1}{2}$.分析 由z=y-x便得到y=x+z,该式可表示在y轴上的截距为z且平行于y=x的直线,这样根据已知条件即可画出原不等式表示的平面区域,从而确定出直线kx-y+2=0的方程,从而求出k.
解答 解:z=y-x表示在y轴上截距为z且平行于y=x的直线;
z取最小值-4时,得到直线y=x-4;
画出直线x+y-2=0和y=x-4如下图: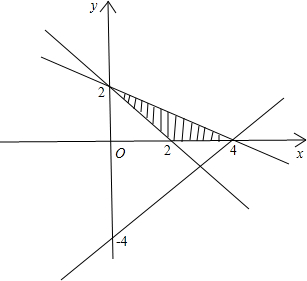
由题意知,直线z=y-x经过原不等式所表示的平面区域的最右端(4,0)点;
从而可知原不等式表示的平面区域如上图阴影部分所示;
∴直线kx-y+2=0表示在x轴上的截距为4,在y轴上的截距为2的直线;
∴y=0时,x=$-\frac{2}{k}$=4;
∴$k=-\frac{1}{2}$.
故答案为:$-\frac{1}{2}$.
点评 考查不等式表示一个平面区域,并根据不等式可找出它表示的平面区域,知道z=y-x可以看成在y轴上截距为z且平行于直线y=x的直线系.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
7.设i是虚数单位,若z=cosθ+isinθ且对应的点位于复平面的第二象限,则θ位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.已知全集U=R,A={x|x<1},B={y|-|x|+y=2},则集合∁U(A∪B)=( )
| A. | {x|1≤x<2} | B. | {x|1<x≤2} | C. | {x|x≥1} | D. | {x|x≤2} |
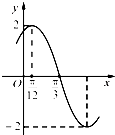 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的个数是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的个数是( )