题目内容
设函数f(x)=|2x+1|-|x-4|.
(1)解不等式f(x)>2;
(2)求函数y=f(x)的最小值.
(1)解不等式f(x)>2;
(2)求函数y=f(x)的最小值.
(1)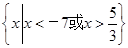 (2)-
(2)-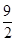
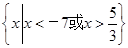 (2)-
(2)-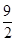
(1)f(x)=|2x+1|-|x-4|=
当x<-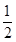 时,由f(x)=-x-5>2得x<-7,∴x<-7;
时,由f(x)=-x-5>2得x<-7,∴x<-7;
当-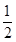 ≤x<4时,由f(x)=3x-3>2得x>
≤x<4时,由f(x)=3x-3>2得x>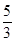 ,∴
,∴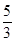 <x<4;
<x<4;
当x≥4时,由f(x)=x+5>2,得x>-3,∴x≥4.
故原不等式的解集为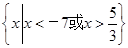 .
.
(2)画出f(x)的图象如图:
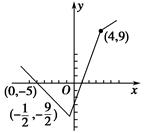
∴f(x)min=-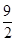 .
.

当x<-
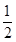 时,由f(x)=-x-5>2得x<-7,∴x<-7;
时,由f(x)=-x-5>2得x<-7,∴x<-7;当-
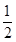 ≤x<4时,由f(x)=3x-3>2得x>
≤x<4时,由f(x)=3x-3>2得x>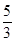 ,∴
,∴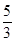 <x<4;
<x<4;当x≥4时,由f(x)=x+5>2,得x>-3,∴x≥4.
故原不等式的解集为
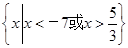 .
.(2)画出f(x)的图象如图:

∴f(x)min=-
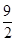 .
.
练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
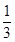 ,|2x-y|<
,|2x-y|<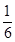 ,求证:|y|<
,求证:|y|<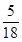 .
.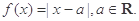
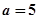 ,解不等式
,解不等式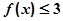 ;
;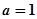 时,若
时,若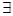
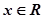 ,使得不等式
,使得不等式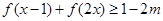 成立,求实数
成立,求实数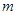 的取值范围.
的取值范围.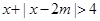 恒成立,则实数
恒成立,则实数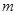 的取值范围是: ;
的取值范围是: ; 和
和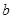 不等式
不等式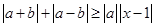 恒成立,则实数x的取值范围是_________.
恒成立,则实数x的取值范围是_________.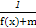 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围. 的不等式
的不等式 的解集是空集,则实数a的取值范围是( )
的解集是空集,则实数a的取值范围是( )



 的方程
的方程 有实根,则
有实根,则 的取值范围是 .
的取值范围是 .