题目内容
设函数f(x)=|2x-1|+|2x-3|,x∈R.
(1)求关于x的不等式f(x)≤5的解集.
(2)若g(x)=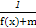 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围.
(1)求关于x的不等式f(x)≤5的解集.
(2)若g(x)=
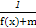 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围.(1) x∈[- ,
, ] (2) m>-2
] (2) m>-2
 ,
, ] (2) m>-2
] (2) m>-2(1)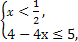 或
或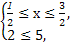 或
或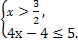
不等式的解集为x∈[- ,
, ].
].
(2)若g(x)=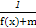 的定义域为R.
的定义域为R.
则f(x)+m≠0恒成立,即f(x)+m=0在R上无解,
又f(x)=|2x-1|+|2x-3|≥|2x-1-2x+3|=2,
f(x)的最小值为2,所以m>-2.
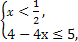 或
或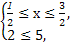 或
或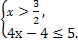
不等式的解集为x∈[-
 ,
, ].
].(2)若g(x)=
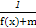 的定义域为R.
的定义域为R.则f(x)+m≠0恒成立,即f(x)+m=0在R上无解,
又f(x)=|2x-1|+|2x-3|≥|2x-1-2x+3|=2,
f(x)的最小值为2,所以m>-2.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
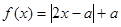 .
.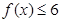 的解集为
的解集为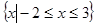 ,求实数a的值;(5分)
,求实数a的值;(5分)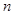 使
使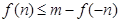 成立,求实数
成立,求实数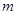 的取值范围.(5分)
的取值范围.(5分)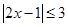 的解集为( )
的解集为( )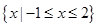
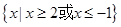
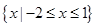
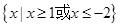
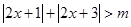 恒成立,则实数
恒成立,则实数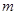 的取值范围为 _______;
的取值范围为 _______;  的解集为 .
的解集为 .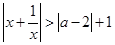 对于一切非零实数
对于一切非零实数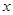 均成立,则实数
均成立,则实数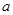 的取值范围是( )
的取值范围是( )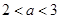
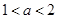
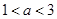
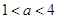
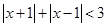 的实数解为 ____________
的实数解为 ____________