题目内容
已知实数x,y满足:|x+y|<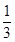 ,|2x-y|<
,|2x-y|<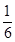 ,求证:|y|<
,求证:|y|<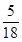 .
.
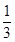 ,|2x-y|<
,|2x-y|<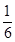 ,求证:|y|<
,求证:|y|<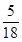 .
.见解析
解 因为3|y|=|3y|=|2(x+y)-(2x-y)|≤2|x+y|+|2x-y|,
由题设知,|x+y|<
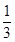 ,|2x-y|<
,|2x-y|<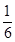 ,
,从而3|y|<
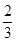 +
+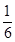 =
=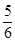 ,所以|y|<
,所以|y|<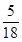 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
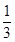 ,|2x-y|<
,|2x-y|<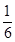 ,求证:|y|<
,求证:|y|<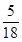 .
.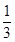 ,|2x-y|<
,|2x-y|<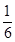 ,
,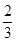 +
+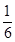 =
=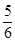 ,所以|y|<
,所以|y|<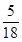 .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案