题目内容
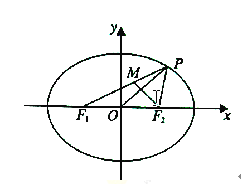
【题目】如图所示,已知椭圆![]() :
:![]() ,其中
,其中![]() ,
,![]() ,
,![]() 分别为其左,右焦点,点
分别为其左,右焦点,点![]() 是椭圆
是椭圆![]() 上一点,
上一点,![]() ,且
,且![]() .
.
(1)当![]() ,
,![]() ,且
,且![]() 时,求
时,求![]() 的值;
的值;
(2)若![]() ,试求椭圆
,试求椭圆![]() 离心率
离心率![]() 的范围.
的范围.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析: (1)先根据![]() 确定点
确定点![]() 坐标,由
坐标,由![]() 可得点
可得点![]() 坐标(用
坐标(用![]() 表示),最后根据
表示),最后根据![]() ,利用斜率乘积为
,利用斜率乘积为![]() ,列方程求
,列方程求![]() 的值;(2)设
的值;(2)设![]() ,由
,由![]() 可得点
可得点![]() 坐标(用
坐标(用![]() 表示),由
表示),由![]() ,得
,得![]() 一组关系,再根据点
一组关系,再根据点![]() 在椭圆
在椭圆![]() 上,可解得
上,可解得![]() (用
(用![]() 表示),最后根据
表示),最后根据![]() 取值范围建立
取值范围建立![]() 之间关系,求得离心率
之间关系,求得离心率![]() 的范围.
的范围.
试题解析:(1)当![]() ,
,![]() 时,椭圆
时,椭圆![]() 为:
为:![]() ,
,![]() ,
,![]() ,
,
∴![]() ,则
,则![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
直线![]() :
:![]() ,①
,①
直线![]() :
:![]() ,②
,②
联立①②解得![]() ,
,
∴![]() .
.
同理可得当![]() 时,
时,![]() ,
,
综上所述,![]() .
.
(2)设![]() ,
,![]() ,
,
由![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
由![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,③
,③
又![]() ,④
,④
联立③④解得![]() (舍)或
(舍)或![]() (∵
(∵![]() ),
),
∴![]() ,即
,即![]() ,
,
∴![]() ,故
,故![]() .
.

练习册系列答案
相关题目