Question

【题目】命题p：关于x的不等式的解集为；命题q：函数为增函数．命题r：a满足．

（1）若p∨q是真命题且p∧q是假题．求实数a的取值范围．

（2）试判断命题￢p是命题r成立的一个什么条件．

Answer 1

【答案】(1) ﹣1≤a＜﹣或＜a≤1；(2) 充分不必要条件

【解析】试题分析：利用判别式求出为真时的取值范围，根据指数函数的图象与性质求出为真时的取值范围，由是真命题且是假命题知一真一假，由此求出的范围。

解不等式得出命题为真时的取值范围，根据集合的包含关系判断命题是命题成立的充分不必要条件。

解析：关于x的不等式x2+（a﹣1）x+a2≤0的解集为，

∴△=（a﹣1）2﹣4a2＜0，

即3a2+2a﹣1＞0，

解得a＜﹣1或a＞，

∴p为真时a＜﹣1或a＞；

又函数y=（2a2﹣a）x为增函数，

∴2a2﹣a＞1，

即2a2﹣a﹣1＞0，

解得a＜﹣或a＞1，

∴q为真时a＜﹣或a＞1；

（1）∵p∨q是真命题且p∧q是假命题，∴p、q一真一假，

∴当P假q真时，，即﹣1≤a＜﹣；

当p真q假时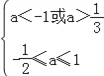，，即＜a≤1；

∴p∨q是真命题且p∧q是假命题时，a的范围是﹣1≤a＜﹣或＜a≤1；

（2）∵，

∴﹣1≤0，

即，

解得﹣1≤a＜2，

∴a∈[﹣1，2），

∵p为真时﹣1≤a≤，

由[﹣1，）是[﹣1，2）的真子集，

∴pr，且r≠＞p，

∴命题p是命题r成立的一个充分不必要条件．