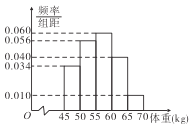
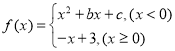题目内容
【题目】某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需要增加投入100元,已知总收益满足函数:R(x)=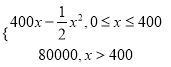 其中x是仪器的月产量.当月产量为何值时,公司所获得利润最大?最大利润是多少?
其中x是仪器的月产量.当月产量为何值时,公司所获得利润最大?最大利润是多少?
【答案】当月产量为300台时,公司所获利润最大,最大利润是25 000元.
【解析】试题分析:一般要根据题意写出利润关于产量的函数,注意不同条件对应利润不同,所以要写成分段函数,然后利用二次函数性质求最值,分段函数最值注意比较两段的最值得大小.
试题解析:(1)设月产量为x台,则总成本为20000+ 100x,从而利润
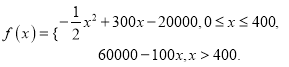
当0≦x≦400时,f(x)= ![]() 所以当x=300时,有最大值25000;
所以当x=300时,有最大值25000;
当x>400时,f(x)=60000-100x是减函数,
所以f(x)= 60000-100×400<25000。
所以当x=300时,有最大值25000,
即当月产量为300台时,公司所获利润最大,最大利润是25000元.

练习册系列答案
相关题目