题目内容
(本小题满分12分)
设椭圆 的离心率
的离心率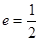 ,右焦点到直线
,右焦点到直线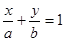 的距离
的距离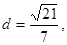
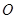 为坐标原点。
为坐标原点。
(I)求椭圆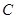 的方程;
的方程;
(II)过点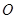 作两条互相垂直的射线,与椭圆
作两条互相垂直的射线,与椭圆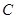 分别交于
分别交于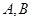 两点,证明点
两点,证明点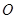 到直线
到直线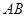 的距离为定值,并求弦
的距离为定值,并求弦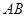 长度的最小值.
长度的最小值.
设椭圆
 的离心率
的离心率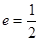 ,右焦点到直线
,右焦点到直线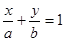 的距离
的距离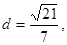
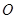 为坐标原点。
为坐标原点。(I)求椭圆
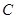 的方程;
的方程;(II)过点
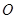 作两条互相垂直的射线,与椭圆
作两条互相垂直的射线,与椭圆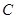 分别交于
分别交于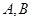 两点,证明点
两点,证明点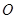 到直线
到直线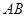 的距离为定值,并求弦
的距离为定值,并求弦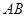 长度的最小值.
长度的最小值.解:(I)由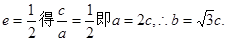
由右焦点到直线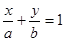 的距离为
的距离为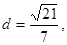
得: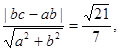 解得
解得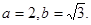
所以椭圆C的方程为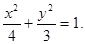 …………4分
…………4分
(II)设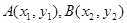 ,
,
直线AB的方程为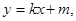 与椭圆
与椭圆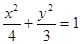 联立消去y得
联立消去y得
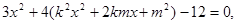
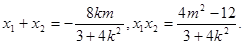
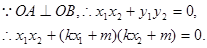
即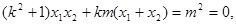
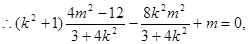
整理得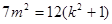 所以O到直线AB的距离
所以O到直线AB的距离
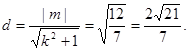 …………8分
…………8分
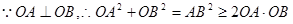 , 当且仅当OA=OB时取“=”号。
, 当且仅当OA=OB时取“=”号。
由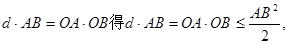
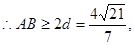
即弦AB的长度的最小值是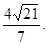 …………12分
…………12分
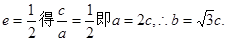
由右焦点到直线
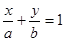 的距离为
的距离为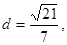
得:
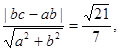 解得
解得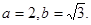
所以椭圆C的方程为
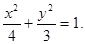 …………4分
…………4分(II)设
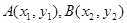 ,
,直线AB的方程为
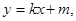 与椭圆
与椭圆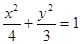 联立消去y得
联立消去y得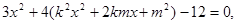
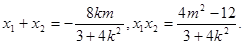
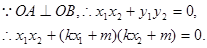
即
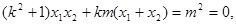
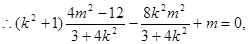
整理得
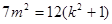 所以O到直线AB的距离
所以O到直线AB的距离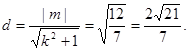 …………8分
…………8分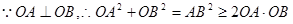 , 当且仅当OA=OB时取“=”号。
, 当且仅当OA=OB时取“=”号。由
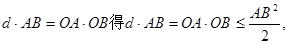
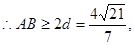
即弦AB的长度的最小值是
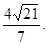 …………12分
…………12分略

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
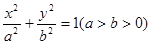 的右焦点为
的右焦点为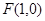 ,
,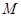 为椭圆的上顶点,
为椭圆的上顶点,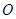 为坐标原点,且△
为坐标原点,且△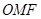 是等腰直角三角形.
是等腰直角三角形.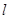 交椭圆于
交椭圆于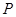 ,
,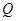 两点, 且使点
两点, 且使点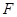 为△
为△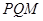 的垂心(垂心:三角形三边高线的交点)?若存在,求出直线
的垂心(垂心:三角形三边高线的交点)?若存在,求出直线 是椭圆
是椭圆 的两个焦点,
的两个焦点, 是椭圆上的动点(不能重合于长轴的两端点),
是椭圆上的动点(不能重合于长轴的两端点), 是
是 的内心,直线
的内心,直线 交
交 轴于点
轴于点 ,则
,则
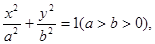 它的一个焦点与抛物线
它的一个焦点与抛物线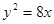 的焦点重合,离心率
的焦点重合,离心率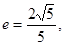 过椭圆的右焦点F作与坐标轴不垂直的直线
过椭圆的右焦点F作与坐标轴不垂直的直线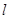 交椭圆于A、B两点.(Ⅰ)求椭圆的标准方程;
交椭圆于A、B两点.(Ⅰ)求椭圆的标准方程;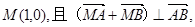 求直线
求直线 的左右焦点分别为
的左右焦点分别为 ,线段
,线段 被抛物线
被抛物线 的焦点
的焦点 内分成了
内分成了 的两段.
的两段. 的直线
的直线 交椭圆于不同两点
交椭圆于不同两点 、
、 ,且
,且 ,当
,当 的面积最大时,求直线
的面积最大时,求直线 的方程.
的方程.
 .
. ,直线l1与椭圆分别交于点M,N,直线l2与椭圆分别交于点P,Q,且
,直线l1与椭圆分别交于点M,N,直线l2与椭圆分别交于点P,Q,且 ,求四边形MPNQ的面积S的最小值.
,求四边形MPNQ的面积S的最小值.
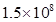 km,半焦距约为
km,半焦距约为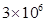 km,则地球到太阳的最大距离是 km。
km,则地球到太阳的最大距离是 km。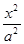 +
+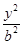 =1(a>b>0),直线y=x+
=1(a>b>0),直线y=x+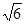 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同 两点A,B且线段AB的垂直平分线过定点C(
两点A,B且线段AB的垂直平分线过定点C(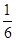 ,0)求实数k的取值范围。
,0)求实数k的取值范围。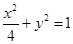 的焦点,P为椭圆上的点,当
的焦点,P为椭圆上的点,当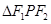 的面积为1时,
的面积为1时,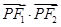 的值是( )
的值是( )