题目内容
已知椭圆C: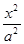 +
+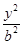 =1(a>b>0),直线y=x+
=1(a>b>0),直线y=x+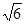 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同 两点A,B且线段AB的垂直平分线过定点C(
两点A,B且线段AB的垂直平分线过定点C(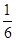 ,0)求实数k的取值范围。
,0)求实数k的取值范围。
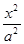 +
+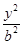 =1(a>b>0),直线y=x+
=1(a>b>0),直线y=x+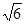 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同 两点A,B且线段AB的垂直平分线过定点C(
两点A,B且线段AB的垂直平分线过定点C(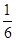 ,0)求实数k的取值范围。
,0)求实数k的取值范围。解:⑴设P(x0,y0),x0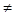 ±a,则G(
±a,则G( ,
, ) ∵IG∥F1F2 ∴Iy=
) ∵IG∥F1F2 ∴Iy= |F1F2|=2c
|F1F2|=2c
∴S△F1PF2=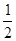 ·|F1F2|·|y0|=
·|F1F2|·|y0|=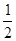 (|PF1|+|PF2|+|F1F2|) · |
(|PF1|+|PF2|+|F1F2|) · | | ……………………(4分)
| ……………………(4分)
∴2c·3="2a+2c " ∴e=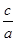 =
=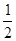 又∵b=
又∵b= ∴b=
∴b=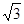 ∴a=2∴椭圆C的方程为
∴a=2∴椭圆C的方程为 +
+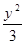 =1(6分)
=1(6分)
⑵设A(x1, y1)、B(x2, y2)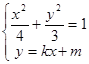 ,消去y (3+4k2)x2+8kmx+4m2-12=0
,消去y (3+4k2)x2+8kmx+4m2-12=0
∴△=(8km)2-4(3+4k2)(4m2-12)>0,即m2<4k2+3又∵x1+x2=- ,则y1+y2=
,则y1+y2=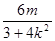
∴线段AB的中点P的坐标为(-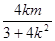 ,
, 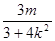 ) …………(8分)
) …………(8分)
又线段AB的垂直平分线l′的方程为y= (x-
(x-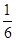 ) …………(9分)
) …………(9分)
点P在直线l′上,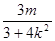 =-
=- (-
(- -
-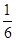 ) …………(10分)
) …………(10分)
∴4k2+6km+3="0 " ∴m=-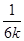 (4k2+3) ∴
(4k2+3) ∴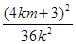 <4k2+3, ∴k2>
<4k2+3, ∴k2>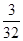
∴k>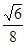 或k>-
或k>- ∴k的取值范围是(-∞,-
∴k的取值范围是(-∞,-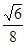 )∪(
)∪(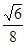 ,+∞) …………(13分)
,+∞) …………(13分)
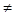 ±a,则G(
±a,则G( ,
, ) ∵IG∥F1F2 ∴Iy=
) ∵IG∥F1F2 ∴Iy= |F1F2|=2c
|F1F2|=2c∴S△F1PF2=
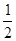 ·|F1F2|·|y0|=
·|F1F2|·|y0|=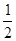 (|PF1|+|PF2|+|F1F2|) · |
(|PF1|+|PF2|+|F1F2|) · | | ……………………(4分)
| ……………………(4分) ∴2c·3="2a+2c " ∴e=
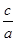 =
=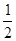 又∵b=
又∵b= ∴b=
∴b=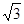 ∴a=2∴椭圆C的方程为
∴a=2∴椭圆C的方程为 +
+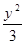 =1(6分)
=1(6分)⑵设A(x1, y1)、B(x2, y2)
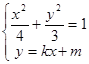 ,消去y (3+4k2)x2+8kmx+4m2-12=0
,消去y (3+4k2)x2+8kmx+4m2-12=0∴△=(8km)2-4(3+4k2)(4m2-12)>0,即m2<4k2+3又∵x1+x2=-
 ,则y1+y2=
,则y1+y2=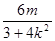
∴线段AB的中点P的坐标为(-
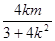 ,
, 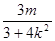 ) …………(8分)
) …………(8分) 又线段AB的垂直平分线l′的方程为y=
 (x-
(x-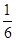 ) …………(9分)
) …………(9分)点P在直线l′上,
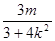 =-
=- (-
(- -
-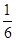 ) …………(10分)
) …………(10分)∴4k2+6km+3="0 " ∴m=-
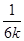 (4k2+3) ∴
(4k2+3) ∴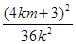 <4k2+3, ∴k2>
<4k2+3, ∴k2>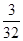
∴k>
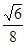 或k>-
或k>- ∴k的取值范围是(-∞,-
∴k的取值范围是(-∞,-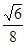 )∪(
)∪(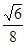 ,+∞) …………(13分)
,+∞) …………(13分)略

练习册系列答案
相关题目
 的离心率
的离心率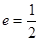 ,右焦点到直线
,右焦点到直线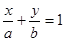 的距离
的距离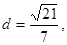
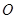 为坐标原点。
为坐标原点。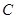 的方程;
的方程;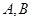 两点,证明点
两点,证明点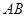 的距离为定值,并求弦
的距离为定值,并求弦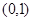 及椭圆
及椭圆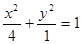 ,Q是椭圆上的动点,则
,Q是椭圆上的动点,则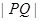 的最大值为
的最大值为  的长轴
的长轴 分成
分成 等份,过每个分点作
等份,过每个分点作 轴的垂线交椭圆的上半部分于
轴的垂线交椭圆的上半部分于 七个点,
七个点, 是椭圆的一个焦点,则
是椭圆的一个焦点,则 ( ).
( ).
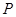 是椭圆
是椭圆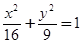 上一点,
上一点,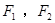 分别是椭圆的左、右焦点,若
分别是椭圆的左、右焦点,若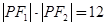 ,则
,则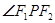 是的大小为( )
是的大小为( )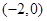 ,
,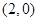 ,且该椭圆过点
,且该椭圆过点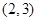 ,则该椭圆的标准方程是_______________
,则该椭圆的标准方程是_______________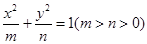 与曲线
与曲线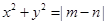 有公共点,则椭圆的离心率
有公共点,则椭圆的离心率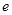 的取值范围是_________________.
的取值范围是_________________.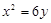 的焦点为F,椭圆C:
的焦点为F,椭圆C: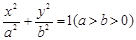 的离心率为
的离心率为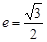 ,
,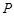 是它们的一个交点,且
是它们的一个交点,且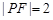 .
.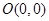 ,点A,B为椭圆
,点A,B为椭圆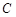 上的两点,且弦AB不平行于对称轴,
上的两点,且弦AB不平行于对称轴,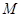 是
是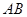 的中点,试探究
的中点,试探究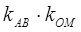 是否为定值,若不是,请说明理由。
是否为定值,若不是,请说明理由。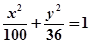 上一点P到它的右准线的距离为10, 则点P到它的左焦点的距离是( )
上一点P到它的右准线的距离为10, 则点P到它的左焦点的距离是( )