题目内容
设 是椭圆
是椭圆 的两个焦点,
的两个焦点, 是椭圆上的动点(不能重合于长轴的两端点),
是椭圆上的动点(不能重合于长轴的两端点), 是
是 的内心,直线
的内心,直线 交
交 轴于点
轴于点 ,则
,则
 是椭圆
是椭圆 的两个焦点,
的两个焦点, 是椭圆上的动点(不能重合于长轴的两端点),
是椭圆上的动点(不能重合于长轴的两端点), 是
是 的内心,直线
的内心,直线 交
交 轴于点
轴于点 ,则
,则
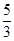
解:因为 是
是 的内心,直线
的内心,直线 交
交 轴于点
轴于点 ,则PD即为角平分线,则利用点I到角的两边距离相等求解。设点P(x0,y0)
,则PD即为角平分线,则利用点I到角的两边距离相等求解。设点P(x0,y0)
设△PF1F2的内切圆半径为r,S△PF1F2="1/" 2 |F1F2|•|y0|="1/" 2 (|PF1|+|PF2|+|F1F2|)•r
于是1/ 2 •2c•|y0|="1" /2 (2a+2c)•r,
又a=2,c=1,y0>0
则r="1" /3 y0,从而I点纵坐标为y0 /3,因此得到
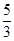
 是
是 的内心,直线
的内心,直线 交
交 轴于点
轴于点 ,则PD即为角平分线,则利用点I到角的两边距离相等求解。设点P(x0,y0)
,则PD即为角平分线,则利用点I到角的两边距离相等求解。设点P(x0,y0)设△PF1F2的内切圆半径为r,S△PF1F2="1/" 2 |F1F2|•|y0|="1/" 2 (|PF1|+|PF2|+|F1F2|)•r
于是1/ 2 •2c•|y0|="1" /2 (2a+2c)•r,
又a=2,c=1,y0>0
则r="1" /3 y0,从而I点纵坐标为y0 /3,因此得到


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,点M(2,1).
,点M(2,1). 的离心率为
的离心率为 ,长轴长为
,长轴长为 ,直线
,直线 交椭圆于不同的两点A、B.
交椭圆于不同的两点A、B. 的值(O点为坐标原点);
的值(O点为坐标原点); 的距离为
的距离为 ,求
,求 面积的最大值.
面积的最大值. 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,且经过点
,且经过点 ,过点
,过点 的直线
的直线 与椭圆
与椭圆 .
. 的方程;
的方程; ?若存在,求出直线
?若存在,求出直线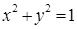 ,点O为坐标原点,一条直线:
,点O为坐标原点,一条直线: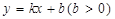 与圆O相切并与椭圆
与圆O相切并与椭圆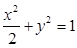 交于不同的两点A、B
交于不同的两点A、B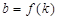 ,求
,求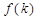 的表达式;
的表达式; 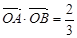 ,求直线的方程;
,求直线的方程;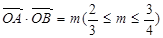 ,求三角形OAB面积的取值范围.
,求三角形OAB面积的取值范围. 的离心率
的离心率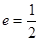 ,右焦点到直线
,右焦点到直线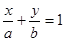 的距离
的距离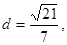
 为坐标原点。
为坐标原点。 的方程;
的方程;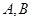 两点,证明点
两点,证明点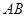 的距离为定值,并求弦
的距离为定值,并求弦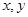 的方程
的方程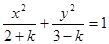 表示焦点在x轴上的椭圆,则
表示焦点在x轴上的椭圆,则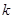 的取值范围为
的取值范围为 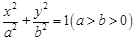 的右焦点为
的右焦点为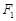 ,右准线为
,右准线为 ,若过点
,若过点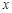 轴的弦的弦长等于点
轴的弦的弦长等于点