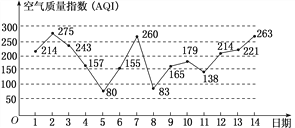
题目内容
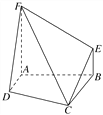
【题目】如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,点E,F,G分别在棱SA,SB,SC上,且平面EFG∥平面ABC,点E为SA的中点.求证:
(Ⅰ)AF⊥平面SBC;
(Ⅱ)SA⊥BC.

【答案】(Ⅰ)见解析(Ⅱ)见解析
【解析】
(Ⅰ)由平面EFG∥平面ABC证得![]() ,即可说明点
,即可说明点![]() 是
是![]() 的中点,即可证得AF⊥SB,利用平面SAB⊥平面SBC即可证得AF⊥平面SBC,问题得证。
的中点,即可证得AF⊥SB,利用平面SAB⊥平面SBC即可证得AF⊥平面SBC,问题得证。
(Ⅱ)由(Ⅰ)中结论可证得BC⊥AF,结合BA⊥BC即可证得BC⊥平面SAB,问题得证。
证明:(Ⅰ)![]() 平面EFG∥平面ABC,
平面EFG∥平面ABC,
平面EFG![]() 平面
平面![]() =
=![]() ,平面ABC
,平面ABC![]() 平面
平面![]() =
=![]() ,
,
![]()
![]() ,又点
,又点![]() 是
是![]() 的中点
的中点
![]() 点
点![]() 是
是![]() 的中点,
的中点,
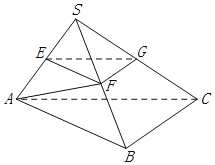
又AS=AB,
![]() AF⊥SB
AF⊥SB
∵在三棱锥S-ABC中,平面SAB⊥平面SBC,平面SAB∩平面SBC=SB,
∴AF⊥平面SBC.
(Ⅱ)∵AF⊥平面SBC,BC平面SBC,
∴BC⊥AF,
∵BA⊥BC.BA∩AF=A,
∴BC⊥平面SAB,
∵SA平面SAB,∴SA⊥BC.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目