题目内容
【题目】若存在一个实数![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的一个不动点,设函数
的一个不动点,设函数![]() (
(![]() ,
, ![]() 为自然对数的底数),定义在
为自然对数的底数),定义在![]() 上的连续函数
上的连续函数![]() 满足
满足![]() ,且当
,且当![]() 时,
时, ![]() .若存在
.若存在![]() ,且
,且![]() 为函数
为函数![]() 的一个不动点,则实数
的一个不动点,则实数![]() 的取值范围为( )
的取值范围为( )
A. 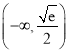 B.
B.  C.
C. 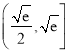 D.
D. 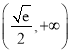
【答案】B
【解析】∵f(﹣x)+f(x)=x2
∴令F(x)=f(x)﹣![]() ,
,
∴f(x)﹣![]() =﹣f(﹣x)+
=﹣f(﹣x)+![]() x2
x2
∴F(x)=﹣F(﹣x),即F(x)为奇函数,
∵F′(x)=f′(x)﹣x,
且当x![]() 0时,f′(x)<x,
0时,f′(x)<x,
∴F′(x)<0对x<0恒成立,
∵F(x)为奇函数,
∴F(x)在R上单调递减,
∵f(x)+![]() ≥f(1﹣x)+x,
≥f(1﹣x)+x,
∴f(x)+![]() ﹣
﹣![]() ≥f(1﹣x)+x﹣
≥f(1﹣x)+x﹣![]() ,
,
即F(x)≥F(1﹣x),
∴x≤1﹣x,
x0≤![]() ,
,
∵![]() 为函数
为函数![]() 的一个不动点
的一个不动点
∴g(x0)=x0,
即h(x)= ![]() =0在(﹣∞,
=0在(﹣∞,![]() ]有解.
]有解.
∵h′(x)=ex-![]() ,
,
∴h(x)在R上单调递减.
∴h(x)min=h(![]() )=
)=![]() ﹣a
﹣a![]() 即可,
即可,
∴a≥![]() .
.
故选:B

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案【题目】自2016年1月1日起,我国全面二孩政策正式实施,这次人口与生育政策的历史性调整,使得“要不要再生一个”,“生二孩能休多久产假”等问题成为千千万万个家庭在生育决策上避不开的话题.为了解针对产假的不同安排方案形成的生育意愿,某调查机构随机抽取了200户有生育二胎能力的适龄家庭进行问卷调查,得到如下数据:
产假安排(单位:周) | 14 | 15 | 16 | 17 | 18 |
有生育意愿家庭数 | 4 | 8 | 16 | 20 | 26 |
(1)若用表中数据所得的频率代替概率,面对产假为14周与16周,估计某家庭有生育意愿的概率分别为多少?
(2)假设从5种不同安排方案中,随机抽取2种不同安排分别作为备选方案,然后由单位根据单位情况自主选择.
①求两种安排方案休假周数和不低于32周的概率;
②如果用![]() 表示两种方案休假周数之和.求随机变量
表示两种方案休假周数之和.求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
【题目】据统计,某5家鲜花店今年4月的销售额和利润额资料如下表:
鲜花店名称 | A | B | C | D | E |
销售额x(千元) | 3 | 5 | 6 | 7 | 9 |
利润额y(千元) | 2 | 3 | 3 | 4 | 5 |
(1)用最小二乘法计算利润额y关于销售额x的回归直线方程![]() =
=![]() x+
x+![]() ;
;
(2)如果某家鲜花店的销售额为8千元时,利用(1)的结论估计这家鲜花店的利润额是多少.
参考公式:回归方程![]() 中斜率和截距的最小二乘法估计值公式分别为
中斜率和截距的最小二乘法估计值公式分别为