Question

【题目】下图是某市11月1日至14日的空气质量指数趋势图，空气质量指数(AQI)小于100表示空气质量优良，空气质量指数大于200表示空气重度污染，某人随机选择11月1日至11月12日中的某一天到达该市，并停留3天．

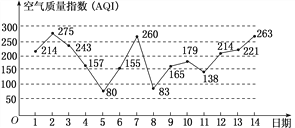
(1)求此人到达当日空气重度污染的概率；

(2)设X是此人停留期间空气重度污染的天数，求X的分布列与数学期望．

Answer 1

【答案】(1)(2)见解析

【解析】试题分析：（1）设Ai表示事件“此人于2月i日到达该市”依题意知p（Ai）=，设B为事件“此人到达当日空气质量重度污染”，则B=A1∪A2∪A3∪A7∪A12，由此能求出此人到达当日空气质量重度污染的概率；

（2）由题意可知，ξ的所有可能取值为0，1，2，3，分别求出P（ξ=0），P（ξ=1），P（ξ=2），P（ξ=3），由此能求出ξ的分布列和ξ的期望．

试题解析：

解：设Ai表示事件“此人于11月i日到达该市”(i＝1，2，…，12)．

依题意知，P(Ai)＝，且Ai∩Aj＝(i≠j)．

(1)设B为事件“此人到达当日空气重度污染”，

则B＝A1∪A2∪A3∪A7∪A12，

所以P(B)＝P(A1∪A2∪A3∪A7∪A12)＝P(A1)＋P(A2)＋P(A3)＋P(A7)＋P(A12)＝.

即此人到达当日空气重度污染的概率为.

(2)由题意可知，X的所有可能取值为0,1,2,3，

P(X＝0)＝P(A4∪A8∪A9)＝P(A4)＋P(A8)＋P(A9)＝＝，

P(X＝2)＝P(A2∪A11)＝P(A2)＋P(A11)＝＝，

P(X＝3)＝P(A1∪A12)＝P(A1)＋P(A12)＝＝，

P(X＝1)＝1－P(X＝0)－P(X＝2)－P(X＝3)＝1－－－＝，

或P(X＝1)＝P(A3∪A5∪A6∪A7∪A10)＝P(A3)＋P(A5)＋P(A6)＋P(A7)＋P(A10)＝

所以X的分布列为：

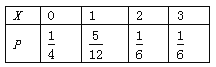
故X的数学期望E(X)＝0×＋1×＋2×＋3×＝.