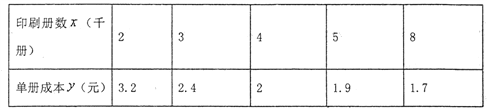
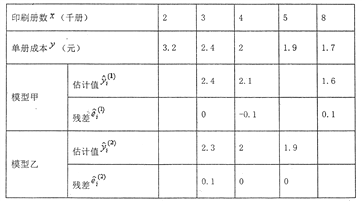
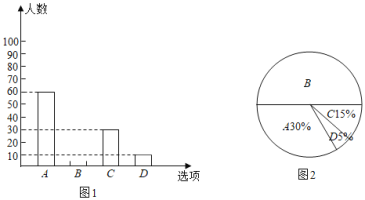
题目内容
【题目】如图,已知AB是圆O的直径,C是圆O上一点,AC=BC,且PA⊥平面ABC,E是AC的中点,F是PB的中点,PA=![]() ,AB=2.求:
,AB=2.求:
(Ⅰ)异面直线EF与BC所成的角;
(Ⅱ)点A到平面PBC的距离.

【答案】(Ⅰ)60°(Ⅱ)![]() .
.
【解析】
(Ⅰ)连接OE,OF,说明∠FEO是异面直线EF与BC所成的角,解三角形![]() 即可。
即可。
(Ⅱ)证明BC⊥平面PAC,即可计算出S△PBC=2,利用等体积法列方程即可得解。
解:(I)连接OE,OF.

∵O是AB的中点,E是AC的中点,
∴OE∥BC,
∴∠FEO是异面直线EF与BC所成的角,
∵O是AB的中点,F是PB的中点,
∴OF∥PA,又PA⊥平面ABC,
∴OF⊥平面ABC,
∵AB是圆O的直径,∴AC⊥BC,
∵AC=BC,AB=2,∴BC=![]() ,∴OE=
,∴OE=![]() BC=
BC=![]() ,
,
又OF=![]() PA=
PA=![]() ,∴tan∠FEO=
,∴tan∠FEO=![]() =
=![]() ,
,
∴异面直线EF与BC所成的角为60°.
(II)∵PA⊥平面ABC,BC平面ABC,
∴PA⊥BC,
∵AB是圆O的直径,∴AC⊥BC,
又PA∩AC=A,
∴BC⊥平面PAC,∴BC⊥PC.
∵PC=![]() =2
=2![]() ,∴S△PBC=
,∴S△PBC=![]() =2.
=2.
设A到平面PBC的距离为h,则VA-PBC=![]() =
=![]() .
.
又VA-PBC=VP-ABC=![]() =
=![]() =
=![]() ,
,
∴h=![]() ,即A到平面PBC的距离为
,即A到平面PBC的距离为![]() .
.

练习册系列答案
相关题目