题目内容
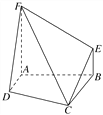
【题目】如图,四边形ABEF和四边形ABCD均是直角梯形,∠FAB=∠DAB=90°,二面角FABD是直二面角,BE∥AF,BC∥AD,AF=AB=BC=2,AD=1.
(1)证明:在平面BCE上,一定存在过点C的直线l与直线DF平行;
(2)求二面角FCDA的余弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)推导出平面BCE∥平面ADF.设平面DFC∩平面BCE=l,则l过点C.由平面BCE∥平面ADF,平面DFC∩平面BCE=l,得到DF∥l,由此能证明在平面BCE上一定存在过点C的直线l,使得DF∥l.(2)以A为原点,AD,AB,AF分别为x轴,y轴,z轴建立空间直角坐标系,利用向量法能求出二面角FCDA的余弦值.
试题解析:
(1)证明:由已知得,BE∥AF,BE平面AFD,AF平面AFD,
∴BE∥平面AFD.
同理可得,BC∥平面AFD.
又BE∩BC=B,∴平面BCE∥平面AFD.
设平面DFC∩平面BCE=l,则l过点C.
∵平面BCE∥平面ADF,平面DFC∩平面BCE=l,平面DFC∩平面AFD=DF,
∴DF∥l,即在平面BCE上一定存在过点C的直线l,使得DF∥l.
(2)∵平面ABEF⊥平面ABCD,平面ABCD∩平面ABEF=AB,FA平面ABEF,
又∠FAB=90°,∴AF⊥AB,∴AF⊥平面ABCD.
∵AD平面ABCD,∴AF⊥AD.
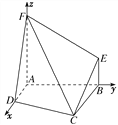
∵∠DAB=90°,∴AD⊥AB.
以A为坐标原点,AD,AB,AF所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,由已知得,D(1,0,0),C(2,2,0),F(0,0,2),∴![]() =(-1,0,2),
=(-1,0,2),![]() =(1,2,0).
=(1,2,0).
设平面DFC的法向量为n=(x,y,z),
则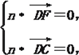 即
即![]()
令z=1,则n=(2,-1,1),
不妨取平面ACD的一个法向量为m=(0,0,1),
∴cos〈m,n〉=![]() =
=![]() =
=![]() ,
,
由于二面角FCDA为锐角,
因此二面角FCDA的余弦值为![]() .
.

【题目】据统计,某5家鲜花店今年4月的销售额和利润额资料如下表:
鲜花店名称 | A | B | C | D | E |
销售额x(千元) | 3 | 5 | 6 | 7 | 9 |
利润额y(千元) | 2 | 3 | 3 | 4 | 5 |
(1)用最小二乘法计算利润额y关于销售额x的回归直线方程![]() =
=![]() x+
x+![]() ;
;
(2)如果某家鲜花店的销售额为8千元时,利用(1)的结论估计这家鲜花店的利润额是多少.
参考公式:回归方程![]() 中斜率和截距的最小二乘法估计值公式分别为
中斜率和截距的最小二乘法估计值公式分别为





