题目内容
1.设正数列{an}的前n项何为Sn,满足Sn=$\frac{1}{4}$(an+1)2,(1)求数列{an}的通项公式;
(2)设bn=$\frac{1}{{a}_{n}{a}_{n+1}}$,记数列{bn}前n项和为Tn,求Tn..
分析 (1)利用an+1=Sn+1-Sn计算、整理可得an+1-an=2,进而计算可得结论;
(2)通过裂项可知bn=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),并项相加即得结论.
解答 解:(1)∵Sn=$\frac{1}{4}$(an+1)2,
∴an+1=Sn+1-Sn
=$\frac{1}{4}$(an+1+1)2-$\frac{1}{4}$(an+1)2
=$\frac{1}{4}$${{a}_{n+1}}^{2}$-$\frac{1}{4}$${{a}_{n}}^{2}$+$\frac{1}{2}$an+1-$\frac{1}{2}$an,
∴$\frac{1}{2}$(an+1+an)=$\frac{1}{4}$${{a}_{n+1}}^{2}$-$\frac{1}{4}$${{a}_{n}}^{2}$=$\frac{1}{4}$(an+1+an)(an+1-an),
又∵an>0,
∴an+1-an=2,
又∵a1=S1=$\frac{1}{4}$(a1+1)2,
∴a1=1,
∴数列{an}是以1为首项、2为公差的等差数列,
∴an=1+2(n-1)=2n-1;
(2)∵an=2n-1,
∴bn=$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
∴Tn=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)
=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)
=$\frac{n}{2n+1}$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

 在电脑游戏中,“主角”的生命机会往往被预先设定.如某枪战游戏,“主角”被设置生命6次,每次生命承受射击8次(即被击中8次就失去一次生命机会),假设射击为单发射击,如图是为“主角”耗用生命机会的过程设计的一个程序框图,请问判断框内应该填( )
在电脑游戏中,“主角”的生命机会往往被预先设定.如某枪战游戏,“主角”被设置生命6次,每次生命承受射击8次(即被击中8次就失去一次生命机会),假设射击为单发射击,如图是为“主角”耗用生命机会的过程设计的一个程序框图,请问判断框内应该填( )| A. | i<6 | B. | i<8 | C. | i>48 | D. | i<48 |
| A. | -$\frac{119}{169}$ | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{119}{169}$ |
| A. | 15 | B. | 10 | C. | 7.5 | D. | 5 |
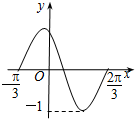
| A. | y=sin(x+$\frac{π}{3}$) | B. | y=sin(2x+$\frac{π}{3}$) | C. | y=sin(2x-$\frac{π}{3}$) | D. | y=sin(2x+$\frac{2π}{3}$) |