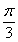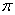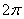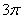题目内容
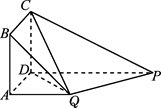
在球面上有四个点P、A、B、C,如果PA、PB、PC两两互相垂直,且PA=PB=PC=a.则这个球的表面积为( )
A.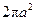
B.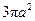
C.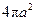
D.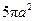
A.
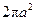
B.
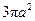
C.
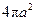
D.
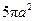
B
设过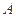 、
、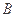 、
、 三点的球的截面半径为
三点的球的截面半径为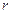 ,
,
球心到该圆面的距离为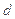 ,
,
则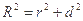 .
.
由题意知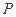 、
、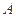 、
、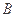 、
、 四点不共面,因而是以这四个点为顶点的三棱锥
四点不共面,因而是以这四个点为顶点的三棱锥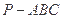 (如图所示).
(如图所示).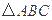 的外接圆是球的截面圆.
的外接圆是球的截面圆.

由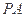 、
、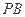 、
、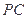 互相垂直知,
互相垂直知,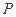 在
在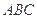 面上的射影
面上的射影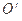 是
是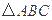 的垂心,又
的垂心,又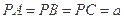 ,
,
所以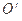 也是
也是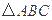 的外心,所以
的外心,所以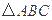 为等边三角形,
为等边三角形,
且边长为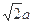 ,
,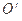 是其中心,
是其中心,
从而也是截面圆的圆心.
据球的截面的性质,有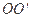 垂直于⊙
垂直于⊙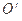 所在平面,
所在平面,
因此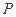 、
、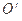 、
、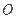 共线,三棱锥
共线,三棱锥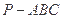 是高为
是高为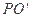 的球内接正三棱锥,从而
的球内接正三棱锥,从而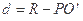 .由已知得
.由已知得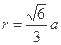 ,
,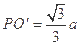 ,所以
,所以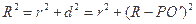 ,可求得
,可求得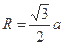 ,∴
,∴ ,选B
,选B
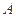 、
、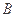 、
、 三点的球的截面半径为
三点的球的截面半径为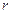 ,
,球心到该圆面的距离为
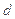 ,
,则
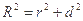 .
.由题意知
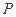 、
、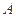 、
、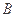 、
、 四点不共面,因而是以这四个点为顶点的三棱锥
四点不共面,因而是以这四个点为顶点的三棱锥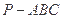 (如图所示).
(如图所示).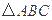 的外接圆是球的截面圆.
的外接圆是球的截面圆.
由
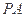 、
、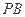 、
、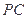 互相垂直知,
互相垂直知,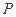 在
在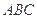 面上的射影
面上的射影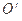 是
是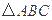 的垂心,又
的垂心,又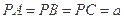 ,
,所以
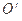 也是
也是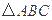 的外心,所以
的外心,所以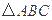 为等边三角形,
为等边三角形,且边长为
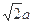 ,
, 是其中心,
是其中心,从而也是截面圆的圆心.
据球的截面的性质,有
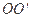 垂直于⊙
垂直于⊙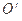 所在平面,
所在平面,因此
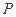 、
、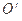 、
、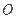 共线,三棱锥
共线,三棱锥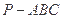 是高为
是高为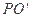 的球内接正三棱锥,从而
的球内接正三棱锥,从而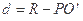 .由已知得
.由已知得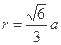 ,
,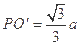 ,所以
,所以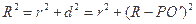 ,可求得
,可求得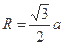 ,∴
,∴ ,选B
,选B
练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
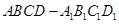 中,底面
中,底面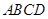 是边长为
是边长为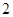 的正方形,
的正方形, 为
为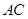 与
与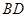 的交点,
的交点,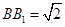 ,
,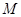 是线段
是线段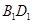 的中点.
的中点.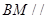 平面
平面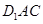 ;
;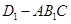 的体积.
的体积.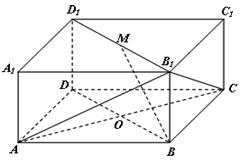
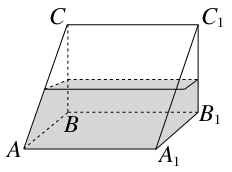
 中,
中, 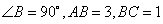 ,以边
,以边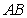 所在直线为旋转轴,其余各边旋转一周而形成的曲面所围成的几何体的体积为( )
所在直线为旋转轴,其余各边旋转一周而形成的曲面所围成的几何体的体积为( )