题目内容
【题目】如图,四棱锥 ![]() 中,底面ABCD为矩形,侧面PAD为正三角形,且平面
中,底面ABCD为矩形,侧面PAD为正三角形,且平面 ![]() ABCD平面, E为PD中点, AD=2.
ABCD平面, E为PD中点, AD=2.
(Ⅰ)求证:平面 ![]() 平面PCD;
平面PCD;
(Ⅱ)若二面角 ![]() 的平面角大小
的平面角大小 ![]() 满足
满足 ![]() ,求四棱锥
,求四棱锥 ![]() 的体积.
的体积.
【答案】解:(Ⅰ)取AD中点为O, BC中点为E,
由侧面PAD为正三角形,且平面 ![]() 平面ABCD知
平面ABCD知 ![]() 平面ABCD,故
平面ABCD,故 ![]() ,
,
又 ![]() ,则
,则 ![]() 平面PAD,所以
平面PAD,所以 ![]() ,
,
又 ![]() ,则
,则 ![]() ,又E是PD中点,则
,又E是PD中点,则 ![]() ,
,
由线面垂直的判定定理知 ![]() 平面PCD,
平面PCD,
又 ![]() 平面AEC,故平面
平面AEC,故平面 ![]() 平面PCD.
平面PCD.
(Ⅱ)
如图所示,建立空间直角坐标系 ![]() ,
,
令AB=a,则 ![]() .
.
由(Ⅰ)知 ![]() 为平面PCE的法向量,
为平面PCE的法向量,
令 ![]() 为平面PAC的法向量,
为平面PAC的法向量,
由于 ![]() 均与n垂直,
均与n垂直,
故 ![]() 即
即 ![]() 解得
解得 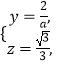
故 ![]() ,由
,由 
 ,解得
,解得 ![]() .
.
故四棱锥 ![]() 的体积
的体积 ![]()
【解析】(1)由平面与平面垂直的性质可得直线与平面垂直,进而得到直线与直线垂直,利用直线与平面垂直的判定定理得到直线与平面垂直,一组相交直线分别垂直于同一平面,故可推出平面与平面垂直。
(2)将立体几何坐标化,通过向量的方法,设出平面法向量,最终求得四棱锥的体积。
【考点精析】根据题目的已知条件,利用平面与平面垂直的判定的相关知识可以得到问题的答案,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直.

练习册系列答案
相关题目


