题目内容
【题目】【2018河南南阳市一中上学期第三次月考】已知点![]() 为坐标原点,
为坐标原点, ![]() 是椭圆
是椭圆![]() 上的两个动点,满足直线
上的两个动点,满足直线![]() 与直线
与直线![]() 关于直线
关于直线![]() 对称.
对称.
(I)证明直线![]() 的斜率为定值,并求出这个定值;
的斜率为定值,并求出这个定值;
(II)求![]() 的面积最大时直线
的面积最大时直线![]() 的方程.
的方程.
【答案】(I)直线![]() 的斜率为定值,其值为
的斜率为定值,其值为![]() ;(II)
;(II)![]() ,或
,或![]() .
.
【解析】试题分析:(1)联立直线和椭圆,解出两个的交点坐标,用两点坐标解出直线斜率![]() ;(2)联立直线和椭圆根据弦长公式得到
;(2)联立直线和椭圆根据弦长公式得到![]() .
.
再根据点到直线的距离得到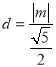 ,此时面积为
,此时面积为![]() ,进而得到结果。
,进而得到结果。
解析:
(1)设直线![]() 方程为:
方程为: ![]() ,代入
,代入![]() 得
得
![]()
设![]() ,因为点
,因为点![]() 在椭圆上,所以
在椭圆上,所以
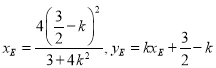
又由题知,直线![]() 的斜率与
的斜率与![]() 的斜率互为相反数,在上式中以
的斜率互为相反数,在上式中以![]() 代
代![]() ,可得
,可得
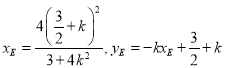 ,
,
所以直线![]() 的斜率
的斜率![]()
即直线![]() 的斜率为定值,其值为
的斜率为定值,其值为![]() .
.
(2)由(1)可设直线![]() 方程为:
方程为: ![]() ,代入
,代入![]() 得
得
![]() ,则
,则![]() .由
.由![]() 可得
可得![]() .
.
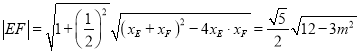 ,
, ![]() 到直线
到直线![]() 的距离
的距离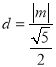 ,
,
可得![]() ,
,
当且仅当![]() (满足
(满足![]() ),即
),即![]() 时取等,此时直线
时取等,此时直线![]() 的方程为:
的方程为: ![]() ,或
,或![]() .
.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目