题目内容
如图,四边形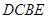 为直角梯形,
为直角梯形,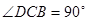 ,
,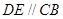 ,
,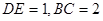 ,又
,又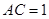 ,
,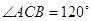 ,
,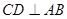 ,直线
,直线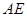 与直线
与直线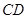 所成角为
所成角为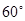 .
.
(Ⅰ)求证:平面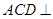 平面
平面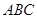 ;
;
(Ⅱ)求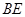 与平面
与平面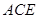 所成角的正弦值.
所成角的正弦值.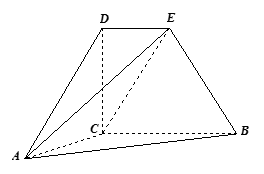
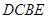 为直角梯形,
为直角梯形,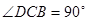 ,
,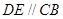 ,
,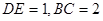 ,又
,又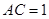 ,
,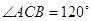 ,
,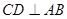 ,直线
,直线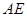 与直线
与直线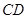 所成角为
所成角为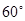 .
.(Ⅰ)求证:平面
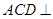 平面
平面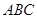 ;
;(Ⅱ)求
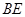 与平面
与平面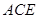 所成角的正弦值.
所成角的正弦值.
(Ⅰ)∵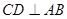 ,
,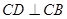 ,
,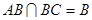 ,
,
∴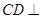 平面
平面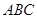 ,
,
又∵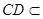 平面
平面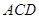 ,
,
∴平面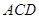
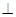 平面
平面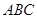 .---------4分
.---------4分
(Ⅱ)在平面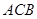 内,过
内,过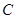 作
作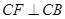 ,以
,以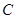 为原点,以
为原点,以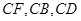 所在射线为
所在射线为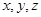 的正半轴建立空间直角坐标系
的正半轴建立空间直角坐标系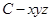 (如图).
(如图).
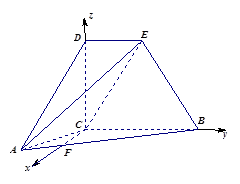
由题意,设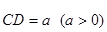 ,
,
则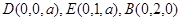 ,
,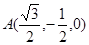 ,
,
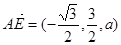 ,
,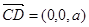 ,---------6分
,---------6分
由直线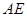 与直线
与直线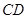 所成角为
所成角为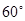 ,得
,得
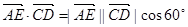 ,即
,即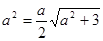 ,解得
,解得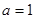 .
.
∴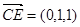 ,
,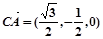 ,
,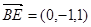 ,
,
设平面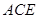 的一个法向量为
的一个法向量为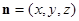 ,则
,则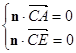 ,
,
即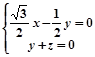 ,取
,取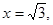 则
则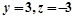 ,得
,得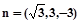 ,
,
设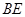 与平面
与平面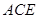 所成角为
所成角为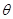 ,则
,则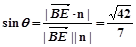 ,于是
,于是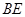 与平面
与平面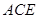 所成角的正弦值为
所成角的正弦值为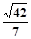
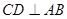 ,
,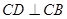 ,
,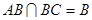 ,
,∴
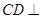 平面
平面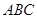 ,
,又∵
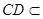 平面
平面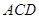 ,
,∴平面
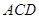
 平面
平面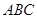 .---------4分
.---------4分(Ⅱ)在平面
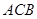 内,过
内,过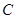 作
作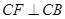 ,以
,以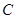 为原点,以
为原点,以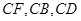 所在射线为
所在射线为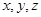 的正半轴建立空间直角坐标系
的正半轴建立空间直角坐标系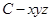 (如图).
(如图).
由题意,设
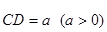 ,
,则
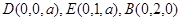 ,
,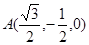 ,
,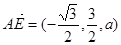 ,
,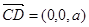 ,---------6分
,---------6分由直线
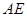 与直线
与直线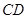 所成角为
所成角为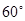 ,得
,得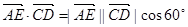 ,即
,即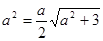 ,解得
,解得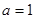 .
.∴
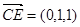 ,
,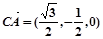 ,
,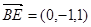 ,
,设平面
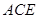 的一个法向量为
的一个法向量为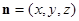 ,则
,则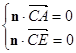 ,
,即
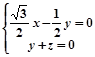 ,取
,取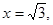 则
则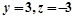 ,得
,得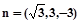 ,
,设
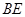 与平面
与平面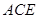 所成角为
所成角为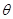 ,则
,则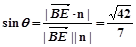 ,于是
,于是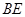 与平面
与平面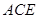 所成角的正弦值为
所成角的正弦值为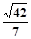
略

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
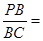
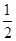 ,
,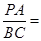
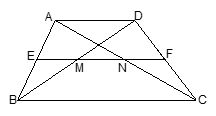
 1
1 中,
中,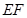 为中位线,对角线
为中位线,对角线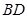 、
、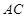 与
与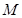 、
、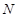 ,如果
,如果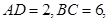 则
则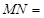 .
. 
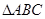 的外接圆的切线
的外接圆的切线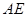 与
与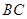 的延长线交于点
的延长线交于点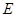 ,
,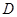 ,满足
,满足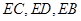 组成等比数列。求证:
组成等比数列。求证: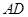 平分
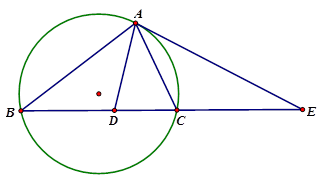
平分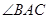 。
。
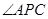 的平分线分别交AB.AC于点D.E.
的平分线分别交AB.AC于点D.E.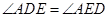 .
.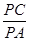 的值.
的值.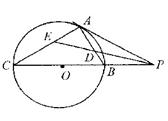
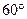 到OD.
到OD. 的线段?若有,指出该线段;若没有,说明理由.
的线段?若有,指出该线段;若没有,说明理由.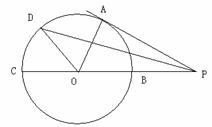
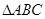 中,AB=BC,以AB为直径的⊙O交AC于点D,过D作
中,AB=BC,以AB为直径的⊙O交AC于点D,过D作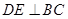 ,垂足为E,连结OE。若
,垂足为E,连结OE。若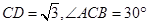 ,分别求AB,OE的长。
,分别求AB,OE的长。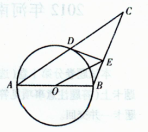
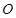 的半径为
的半径为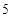
 ,点
,点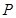 是弦
是弦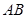 的中点,
的中点,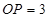
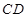 过点
过点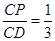 ,则
,则