题目内容
选修4-1:几何证明与选讲
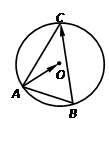
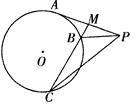
如图,已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B.C,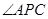 的平分线分别交AB.AC于点D.E.
的平分线分别交AB.AC于点D.E.
(1)证明: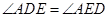 .
.
(2)若AC=AP,求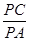 的值.
的值.
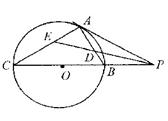
如图,已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B.C,
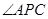 的平分线分别交AB.AC于点D.E.
的平分线分别交AB.AC于点D.E.(1)证明:
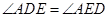 .
.(2)若AC=AP,求
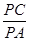 的值.
的值.
(1)∵ PA是切线,AB是弦,
∴ ∠BAP=∠C, ………………………………2分
又 ∵ ∠APD="∠CPE,"
∴ ∠BAP+∠APD=∠C+∠CPE,
∵ ∠ADE="∠BAP+∠APD,"
∠AED="∠C+∠CPE, " …………………………4分
∴ ∠ADE=∠AED. …………………………5分
(2)由(1)知∠BAP="∠C," 又 ∵ ∠APC=∠BPA,
∴ △APC∽△BPA, ∴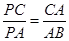 , ……………7分
, ……………7分
∵ AC="AP," ∴ ∠APC=∠C=∠BAP,
由三角形内角和定理可知,∠APC+∠C+∠CAP=180°,
∵ BC是圆O的直径,∴ ∠BAC="90°," ∴ ∠APC+∠C+∠BAP=180°-90°=90°,
∴ ∠C=∠AP C=∠BAP=
C=∠BAP=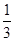 ×90°=30°. ………………………………9分
×90°=30°. ………………………………9分
在Rt△ABC中,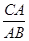 =
=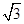 , ∴
, ∴ 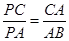 =
=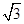 .
.
∴ ∠BAP=∠C, ………………………………2分
又 ∵ ∠APD="∠CPE,"
∴ ∠BAP+∠APD=∠C+∠CPE,
∵ ∠ADE="∠BAP+∠APD,"
∠AED="∠C+∠CPE, " …………………………4分
∴ ∠ADE=∠AED. …………………………5分
(2)由(1)知∠BAP="∠C," 又 ∵ ∠APC=∠BPA,
∴ △APC∽△BPA, ∴
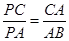 , ……………7分
, ……………7分∵ AC="AP," ∴ ∠APC=∠C=∠BAP,
由三角形内角和定理可知,∠APC+∠C+∠CAP=180°,
∵ BC是圆O的直径,∴ ∠BAC="90°," ∴ ∠APC+∠C+∠BAP=180°-90°=90°,
∴ ∠C=∠AP
 C=∠BAP=
C=∠BAP=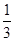 ×90°=30°. ………………………………9分
×90°=30°. ………………………………9分在Rt△ABC中,
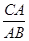 =
=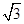 , ∴
, ∴ 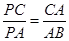 =
=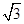 .
.略

练习册系列答案
相关题目
 外一点
外一点 引圆的一条切线
引圆的一条切线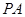 ,切点为
,切点为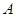 ,
,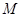 为
为 两点,且
两点,且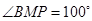 ,
,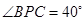 .
.
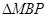 与
与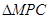 相似;
相似;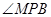 的大小.
的大小.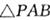 的顶点A、B为定点,P为动点,其内切圆O1与AB、PA、PB分别相切于点C、E、F,且
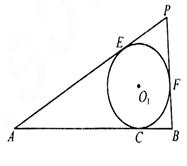
的顶点A、B为定点,P为动点,其内切圆O1与AB、PA、PB分别相切于点C、E、F,且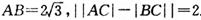 •
•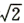 ,若l与曲线W相交于不同的两点G、H,点M满足
,若l与曲线W相交于不同的两点G、H,点M满足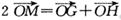 ,证明:
,证明: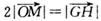
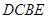 为直角梯形,
为直角梯形,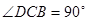 ,
,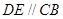 ,
,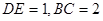 ,又
,又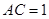 ,
,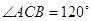 ,
,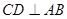 ,直线
,直线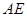 与直线
与直线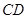 所成角为
所成角为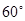 .
.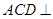 平面
平面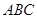 ;
;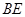 与平面
与平面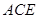 所成角的正弦值.
所成角的正弦值.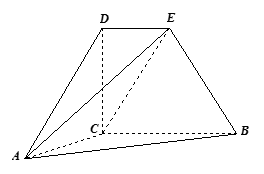
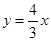 ;③y=2;④y=2x+1.
;③y=2;④y=2x+1.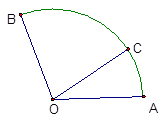
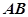
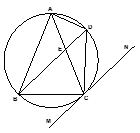
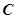 是内接于⊙O,
是内接于⊙O,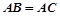 ,直线
,直线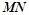 切⊙O于点
切⊙O于点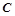 ,弦
,弦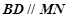 ,
,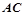 与
与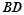 相交于点
相交于点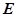 .
.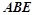 ≌Δ
≌Δ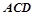 ;
;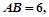
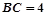 ,求
,求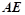 .
.
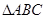 和
和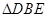 中,
中,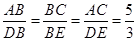 ,若
,若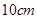 ,则
,则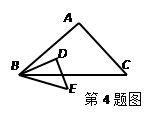
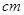 B.
B.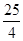
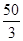
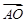 ·
·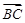 的值是
的值是