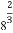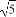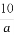Question

已知函数f(x)=loga(3-ax).

(1)当x∈[0,2]时,函数f(x)恒有意义,求实数a的取值范围.

(2)是否存在这样的实数a,使得函数f(x)在区间[1,2]上为减函数,并且最大值为1?如果存在,试求出a的值;如果不存在,请说明理由.

 

Answer 1

(1) (0,1)∪(1,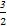) (2) 不存在，理由见解析

【解析】(1)由题设,3-ax>0对一切x∈[0,2]恒成立,设g(x)=3-ax,∵a>0,且a≠1,∴g(x)=3-ax在[0,2]上为减函数.

从而g(2)=3-2a>0,∴a<.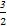

∴a的取值范围为(0,1)∪(1,).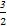

(2)假设存在这样的实数a,

由题设知f(1)=1,

即loga(3-a)=1,∴a=.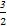

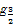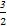此时f(x)=lo(3-x),

当x=2时,f(x)没有意义,故这样的实数a不存在.