Question

下列说法中,不正确的是(　　)

(A)命题p:?x∈R,sinx≤1,则p:?x∈R,sinx>1

(B)在△ABC中,“A>30°”是“sinA>”的必要不充分条件

(C)命题p:点(,0)为函数f(x)=tan(2x+)的一个对称中心;命题q:如果|a|=1,|b|=2,<a,b>=120°,那么b在a方向上的投影为1,则(p)∨(q)为真命题

(D)命题“在△ABC中,若sinA=sinB,则△ABC为等腰三角形”的否命题为真命题

 

Answer 1

D

【解析】根据含有量词命题的否定方法,选项A中的结论正确;在△ABC中,sinA>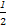时,30°<A<150°,可得A>30°,但A>30°时未必sinA>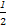,如A=150°>30°,此时sinA=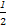,故选项B中的结论正确;当x=时,2x+=,故点(,0)是函数f(x)=tan(2x+)的对称中心,命题p是真命题,向量b在a方向上的投影为|b|cos120°=-1,命题q是假命题,此时(p)∨(q)为真命题,选项C中的结论正确;已知命题的否命题是“在△ABC中,若sinA≠sinB,则△ABC不是等腰三角形”,命题是假命题,如A=90°,B=C=45°,选项D中的说法不正确.