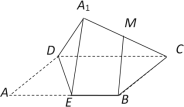
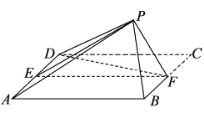
题目内容
【题目】正方形![]() 的边长为2,
的边长为2,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,以
的中点,以![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,平面
的位置,平面![]() 平面
平面![]() .
.
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)利用正方形的性质可得![]() 垂直于面
垂直于面![]() ,得到
,得到![]() 又
又![]() ,所以
,所以![]() 再由已知条件即可证明.
再由已知条件即可证明.
(2)作![]() ,垂足为
,垂足为![]() ,由(1)得,
,由(1)得,![]() 平面
平面![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴正方向,建立如图所示的空间直角坐标系
轴正方向,建立如图所示的空间直角坐标系![]() ,利用空间向量法求出二面角的余弦值.
,利用空间向量法求出二面角的余弦值.
解:(1)由已知可得,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
![]() ,又
,又![]() ,所以
,所以![]() ,又
,又![]() ,
,
且![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)作![]() ,垂足为
,垂足为![]() ,由(1)得,
,由(1)得,![]() 平面
平面![]() .
.
以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴正方向,建立如图所示的空间直角坐标系
轴正方向,建立如图所示的空间直角坐标系![]() .
.
由(1)可得,![]() .又
.又![]() ,
,![]() ,所以
,所以![]() .故
.故![]() .
.
可得![]() ,
,![]() .
.
则![]() ,
,![]() ,
,![]() ,
, ,
,![]() ,
, ,
,![]() ,
,
由(1)知:![]() 为平面
为平面![]() 的法向量,
的法向量, .
.
设平面![]() 的法向量为
的法向量为![]() ,则:
,则: ,即
,即 ,
,
所以![]() ,令
,令![]() ,则
,则![]() ,
,![]() .
.
则 .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .
.


【题目】某机器生产商,对一次性购买两台机器的客户推出两种超过质保期后两年内的延保维修方案:
方案一:交纳延保金![]() 元,在延保的两年内可免费维修
元,在延保的两年内可免费维修![]() 次,超过
次,超过![]() 次每次收取维修费
次每次收取维修费![]() 元;
元;
方案二:交纳延保金![]() 元,在延保的两年内可免费维修
元,在延保的两年内可免费维修![]() 次,超过
次,超过![]() 次每次收取维修费
次每次收取维修费![]() 元.
元.
某工厂准备一次性购买两台这种机器,现需决策在购买机器时应购买哪种延保方案,为此搜集并整理了台这种机器超过质保期后延保两年内维修的次数,统计得下表:
维修次数 | 0 | 1 | 2 | 3 |
机器台数 | 20 | 10 | 40 | 30 |
以上![]() 台机器维修次数的频率代替一台机器维修次数发生的概率,记
台机器维修次数的频率代替一台机器维修次数发生的概率,记![]() 表示这两台机器超过质保期后延保两年内共需维修的次数.
表示这两台机器超过质保期后延保两年内共需维修的次数.
![]() 求
求![]() 的分布列;
的分布列;
![]() 以所需延保金与维修费用之和的期望值为决策依据,该工厂选择哪种延保方案更合算?
以所需延保金与维修费用之和的期望值为决策依据,该工厂选择哪种延保方案更合算?
【题目】在2018年10月考考试中,成都外国语学校共有250名高三文科学生参加考试,数学成绩的频率分布直方图如图:
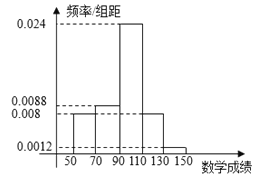
(1)如果成绩大于130的为特别优秀,这250名学生中本次考试数学成绩特别优秀的大约多少人?
(2)如果这次考试语文特别优秀的有5人,语文和数学两科都特别优秀的共有2人,从(1)中的数学成绩特别优秀的人中随机抽取2人,求选出的2人中恰有1名两科都特别优秀的概率.
(3)根据(1),(2)的数据,是否有99%以上的把握认为语文特别优秀的同学,数学也特别优秀?
①![]()
②
P( | 0.50 | 0.40 | … | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | … | 6.635 | 7.879 | 10.828 |
【题目】某部门经统计,客户对不同款型理财产品的最满意程度百分比和对应的理财总销售量(万元)如下表(最满意度百分比超高时总销售量最高):
产品款型 | A | B | C | D | E | F | G | H | I | J |
最满意度% | 20 | 34 | 25 | 19 | 26 | 20 | 19 | 24 | 19 | 13 |
总销量(万元) | 80 | 89 | 89 | 78 | 75 | 71 | 65 | 62 | 60 | 52 |
设![]() 表示理财产品最满意度的百分比,
表示理财产品最满意度的百分比,![]() 为该理财产品的总销售量(万元).这些数据的散点图如图所示.
为该理财产品的总销售量(万元).这些数据的散点图如图所示.
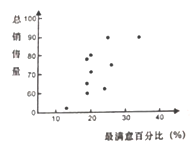
(1)在![]() 份
份![]() 款型理财产品的顾客满意度调查资料中任取
款型理财产品的顾客满意度调查资料中任取![]() 份;只有一份最满意的,求含有最满意客户资料事件的概率.
份;只有一份最满意的,求含有最满意客户资料事件的概率.
(2)我们约定:相关系数的绝对值在![]() 以下是无线性相关,在
以下是无线性相关,在![]() 以上(含
以上(含![]() )至
)至![]() 是一般线性相关,在
是一般线性相关,在![]() 以上(含
以上(含![]() )是较强线性相关,若没有达到较强线性相关则采取“末位”剔除制度(即总销售量最少的那一款产品退出理财销售);试求在剔除“末位”款型后的线性回归方程(系数精确到
)是较强线性相关,若没有达到较强线性相关则采取“末位”剔除制度(即总销售量最少的那一款产品退出理财销售);试求在剔除“末位”款型后的线性回归方程(系数精确到![]() ).
).
数据参考计算值:
项目 |
|
|
|
|
|
|
值 | 21.9 | 72.1 | 288.9 | 37.16 | 452.1 | 17.00 |
附:回归直线方程![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为:
线性相关系数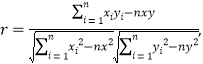
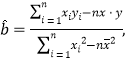
![]() .
.