题目内容
如图,直三棱柱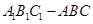 中,
中, 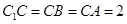 ,
, .
. 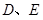 分别为棱
分别为棱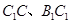 的中点.
的中点.
(1)求二面角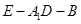 的平面角的余弦值;
的平面角的余弦值;
(2)在线段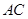 上是否存在一点
上是否存在一点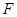 ,使得
,使得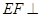 平
平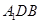 ?
?
若存在,确定其位置;若不存在,说明理由.
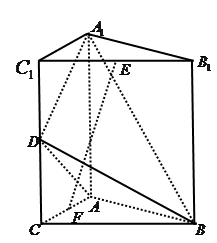
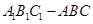 中,
中, 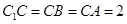 ,
, .
. 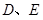 分别为棱
分别为棱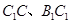 的中点.
的中点.(1)求二面角
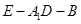 的平面角的余弦值;
的平面角的余弦值;(2)在线段
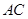 上是否存在一点
上是否存在一点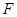 ,使得
,使得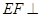 平
平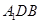 ?
?若存在,确定其位置;若不存在,说明理由.
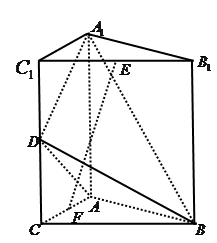
(1)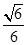 ;(2)见解析.
;(2)见解析.
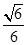 ;(2)见解析.
;(2)见解析.本试题主要是考查了立体几何中的二面角的求解,线面垂直的判定定理的运用。
解:(1)如图所示,以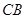 为
为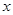 轴,
轴,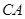 为
为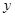 轴,
轴,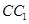 为
为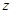 轴建立空间直角坐标系,由
轴建立空间直角坐标系,由
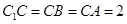 可得
可得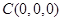 ,
,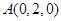 ,
,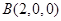 ,
,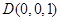 ,
,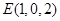 .
.

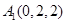 ,
,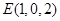 ,
,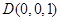 可得
可得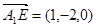 ,
,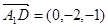 …………2分
…………2分
设平面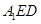 的法向量为
的法向量为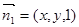
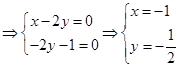 ,
,
故可令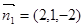 ,
,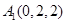 ,
,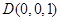 ,
,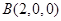 ,
,
可得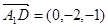 ,
,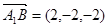 ,
,
设平面 的法向量为
的法向量为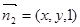
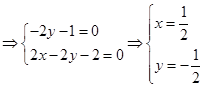 ,
,
故可令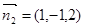 ,∴
,∴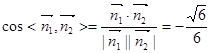 ,
,
即求二面角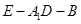 的余弦值为
的余弦值为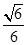 ; ……………8分
; ……………8分
(2)假设存在点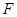 ,坐标为
,坐标为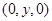 ,则
,则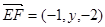 ,
,
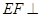 平面
平面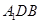 得
得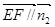 ,即
,即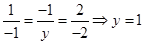 ,
,
∴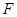
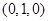
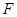 即为
即为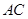 中点. ……………14分
中点. ……………14分
解:(1)如图所示,以
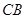 为
为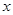 轴,
轴,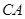 为
为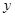 轴,
轴,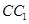 为
为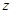 轴建立空间直角坐标系,由
轴建立空间直角坐标系,由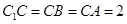 可得
可得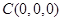 ,
,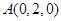 ,
,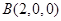 ,
,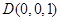 ,
,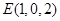 .
.
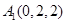 ,
,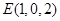 ,
,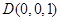 可得
可得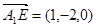 ,
,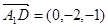 …………2分
…………2分设平面
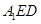 的法向量为
的法向量为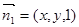
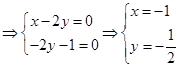 ,
,故可令
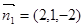 ,
,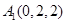 ,
,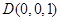 ,
,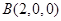 ,
,可得
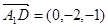 ,
,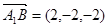 ,
,设平面
 的法向量为
的法向量为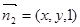
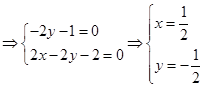 ,
,故可令
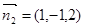 ,∴
,∴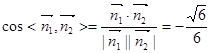 ,
,即求二面角
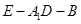 的余弦值为
的余弦值为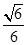 ; ……………8分
; ……………8分(2)假设存在点
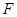 ,坐标为
,坐标为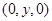 ,则
,则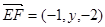 ,
,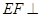 平面
平面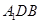 得
得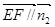 ,即
,即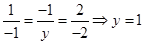 ,
,∴
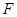
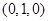
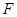 即为
即为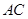 中点. ……………14分
中点. ……………14分
练习册系列答案
相关题目
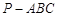 中,
中,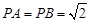 ,
,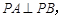
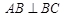 ,
,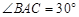 ,平面
,平面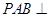 平面
平面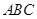 。
。 ;
; 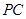 和面
和面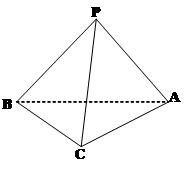
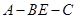 的大小的余弦值.
的大小的余弦值.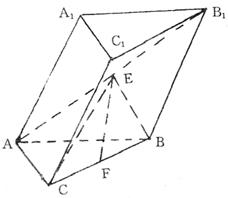
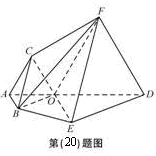
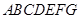 为多面体,平面
为多面体,平面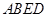 与平面
与平面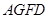 垂直,点
垂直,点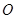 在线段
在线段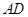 上,
上,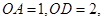 △OAB,,△
△OAB,,△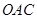 ,△
,△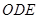 ,△
,△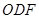 都是正三角形。
都是正三角形。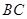 ∥
∥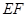 ;
;
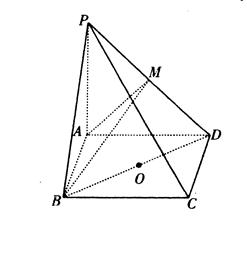
 中,
中, 是
是 的中点,
的中点, 是线段
是线段 上一点,且
上一点,且 .
. ;
; 平面
平面 ,求
,求 的值.[
的值.[
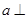 直线
直线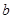 ,a,b异面,
,a,b异面,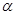 ,
,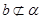 。求证:
。求证: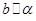 。
。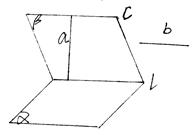
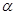 //平面β,点
//平面β,点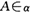 ,直线
,直线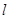 经过点A,则“
经过点A,则“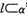 ”是“
”是“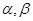 是不重合的平面,则下列条件中可推出a∥b的是( )
是不重合的平面,则下列条件中可推出a∥b的是( )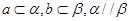 ?
?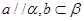
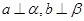 ?
?